In the adjoining figure, a chord PQ of a circle with center O and radius 15 cm is bisected at M by a diameter AB. If OM = 9 cm, find the lengths of :

(i) PQ

(ii) AP

(iii) BP.

(i) Given,

AB bisects PQ.

∴ OM bisects PQ.

Since, the straight line drawn from the centre of a circle to bisect a chord, which is not a diameter, is perpendicular to the chord,

∴ OM ⊥ PQ.

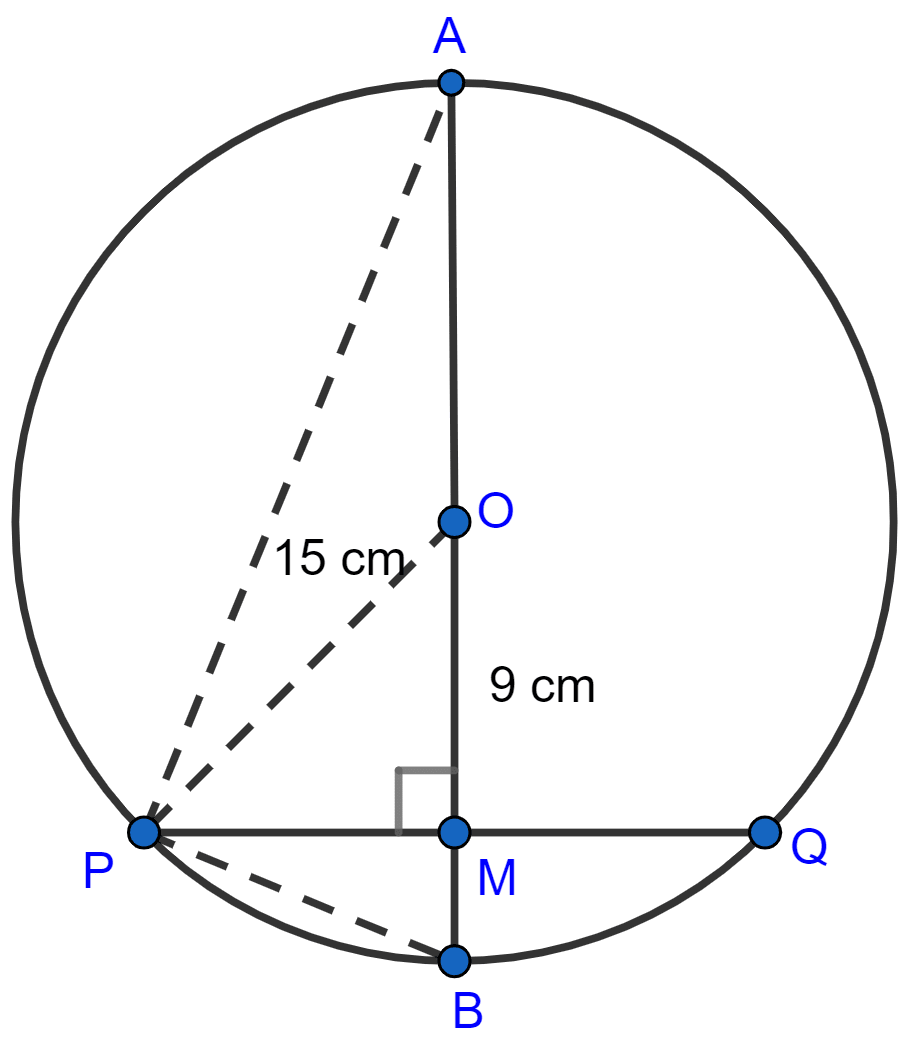
In right △OMP,

⇒ OP² = OM² + PM² (By pythagoras theorem)

⇒ 15² = 9² + PM²

⇒ PM² = 15² - 9²

⇒ PM² = 225 - 81

⇒ PM² = 144

⇒ PM = $\sqrt{144}$ = 12 cm.

PQ = 2PM = 24 cm.

Hence, PQ = 24 cm.

(ii) From figure,

AM = AO + OM = 15 + 9 = 24 cm.

In right △APM,

⇒ AP² = AM² + PM² (By pythagoras theorem)

⇒ AP² = 24² + 12²

⇒ AP² = 576 + 144

⇒ AP² = 720

⇒ AP = $\sqrt{720}$ = $12\sqrt{5}$ cm.

Hence, AP = $12\sqrt{5}$ cm.

(iii) From figure,

MB = OB - OM = 15 - 9 = 6 cm.

In right △MPB,

⇒ BP² = PM² + MB² (By pythagoras theorem)

⇒ BP² = 12² + 6²

⇒ BP² = 144 + 36

⇒ BP² = 180

⇒ BP = $\sqrt{180}$ = $6\sqrt{5}$ cm.

Hence, BP = $6\sqrt{5}$ cm.