Mathematics
A 15 meters high tower casts a shadow of 24 metres long at a certain time and at the same time, a telephone pole casts a shadow 16 meters long. Find the height of the telephone pole.
Similarity
Answer
Let AB be tower and CD be pole.
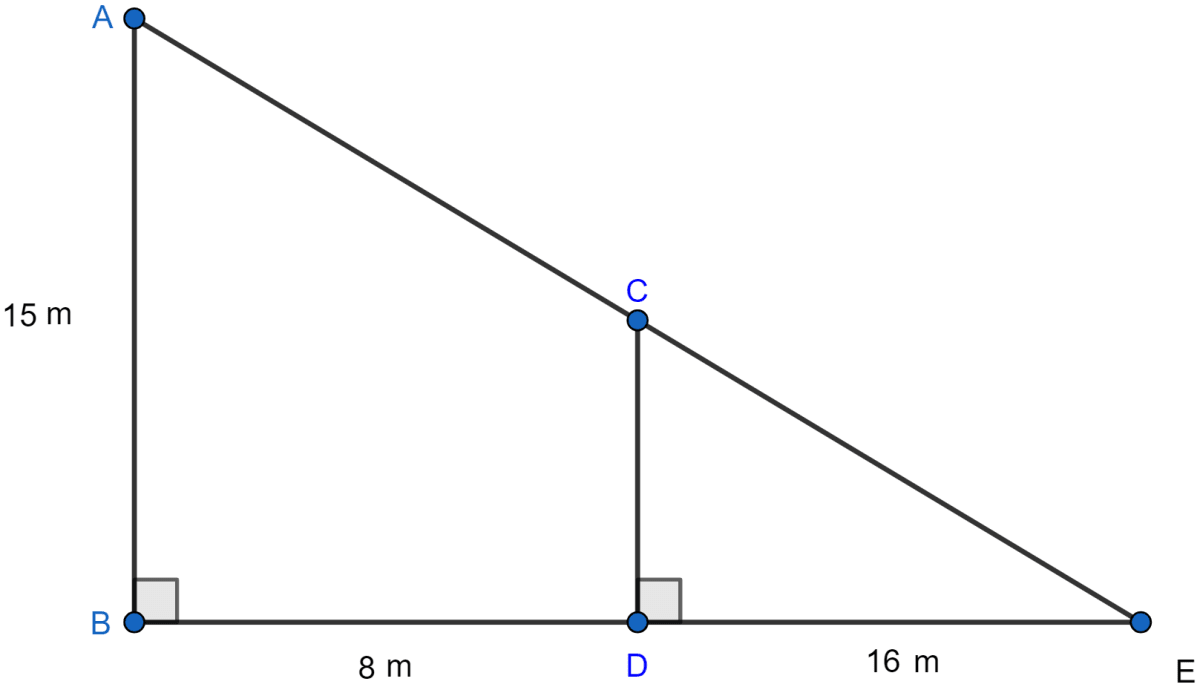
BE = Shadow of tower and
DE = Shadow of telephone pole.
Considering △ABE and △CDE
∠ABE = ∠CDE (Both are equal to 90°)
∠AEB = ∠CED [Common angles]
So, by AA rule of similarity △ABE ~ △CDE. Hence, the ratio of corresponding sides will be equal.
Hence, the height of telephone pole is 10 m.
Answered By
Related Questions
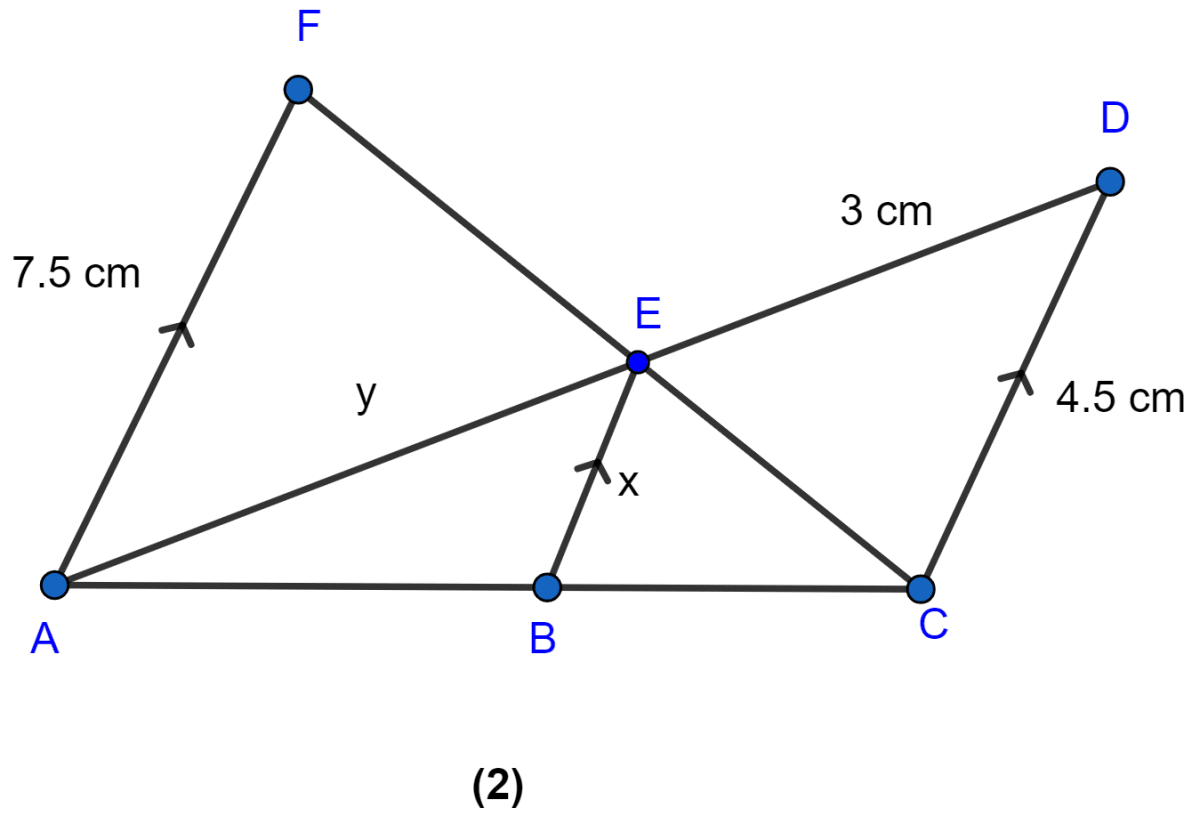
In the figure (2) given below, AF, BE and CD are parallel lines. Given that AF = 7.5 cm, CD = 4.5 cm, ED = 3 cm and BE = x and AE = y. Find the values of x and y.
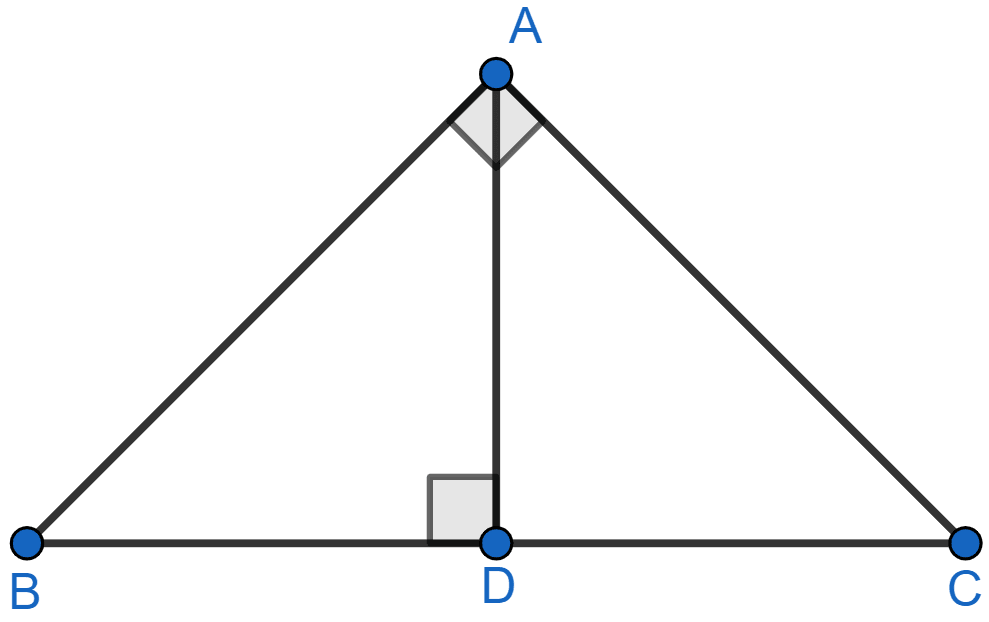
In the given figure, ∠A = 90° and AD ⊥ BC. If BD = 2 cm and CD = 8 cm, find AD.
A street light bulb is fixed on a pole 6m above the level of street. If a woman of height 1.5 m casts a shadow of 3 m, find how far she is away from the base of the pole ?
In the figure (i) given below, if DE ∥ BC, AD = 3 cm, BD = 4 cm and BC = 5 cm, find (i) AE : EC (ii) DE.
