Mathematics
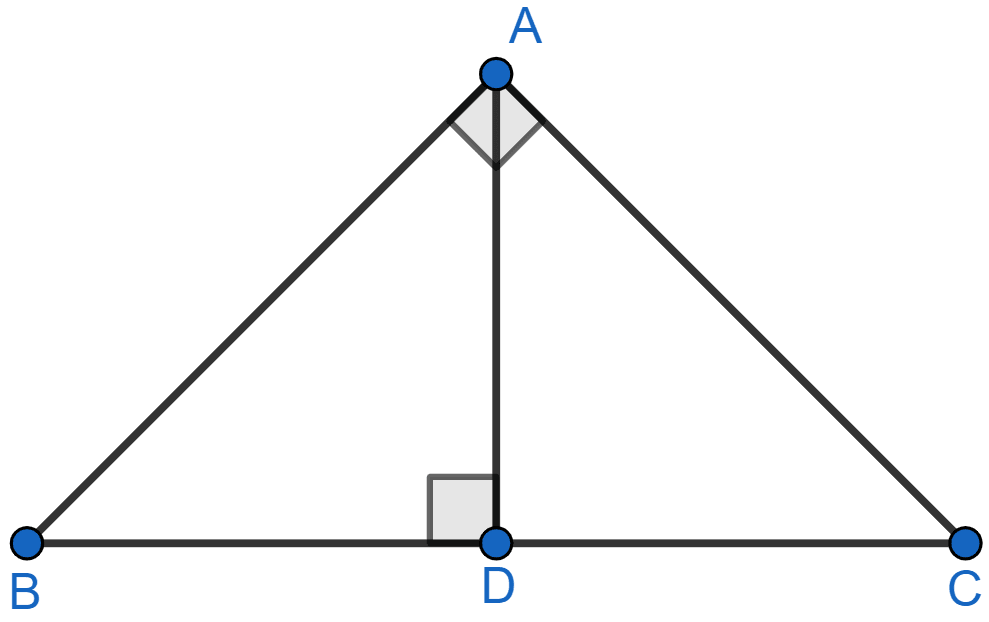
In the given figure, ∠A = 90° and AD ⊥ BC. If BD = 2 cm and CD = 8 cm, find AD.
Similarity
68 Likes
Answer
Given ∠A = 90°,
or, ∠BAD + ∠DAC = 90° …..(i)
Now, consider △ADC
∠ADC = 90°
or, ∠DCA + ∠DAC = 90° …..(ii)
From equation (i) and equation (ii)
We have,
∠BAD + ∠DAC = ∠DCA + ∠DAC
∠BAD = ∠DCA …..(iii)
So, from △BDA and △ADC
∠BDA = ∠ADC = 90°
∠BAD = ∠DCA [From equation (iii)]
So, by AA rule of similarity △BDA ~ △ADC.
Since, corresponding sides of similar triangles are proportional,
Since, length cannot be negative hence, AD ≠ -4.
Hence, the length of AD = 4 cm.
Answered By
27 Likes
Related Questions
In the figure (1) given below, AB, EF and CD are parallel lines. Given that AB = 15 cm, EG = 5 cm, GC = 10 cm and DC = 18 cm. Calculate
(i) EF (ii) AC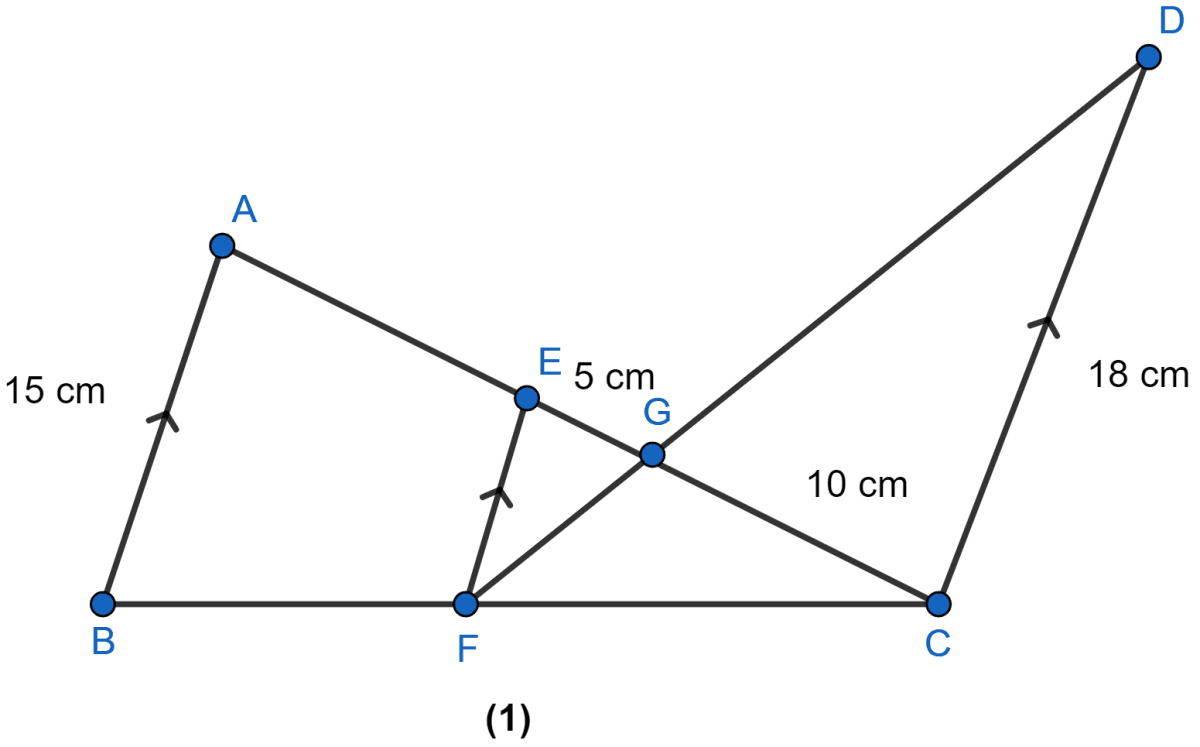
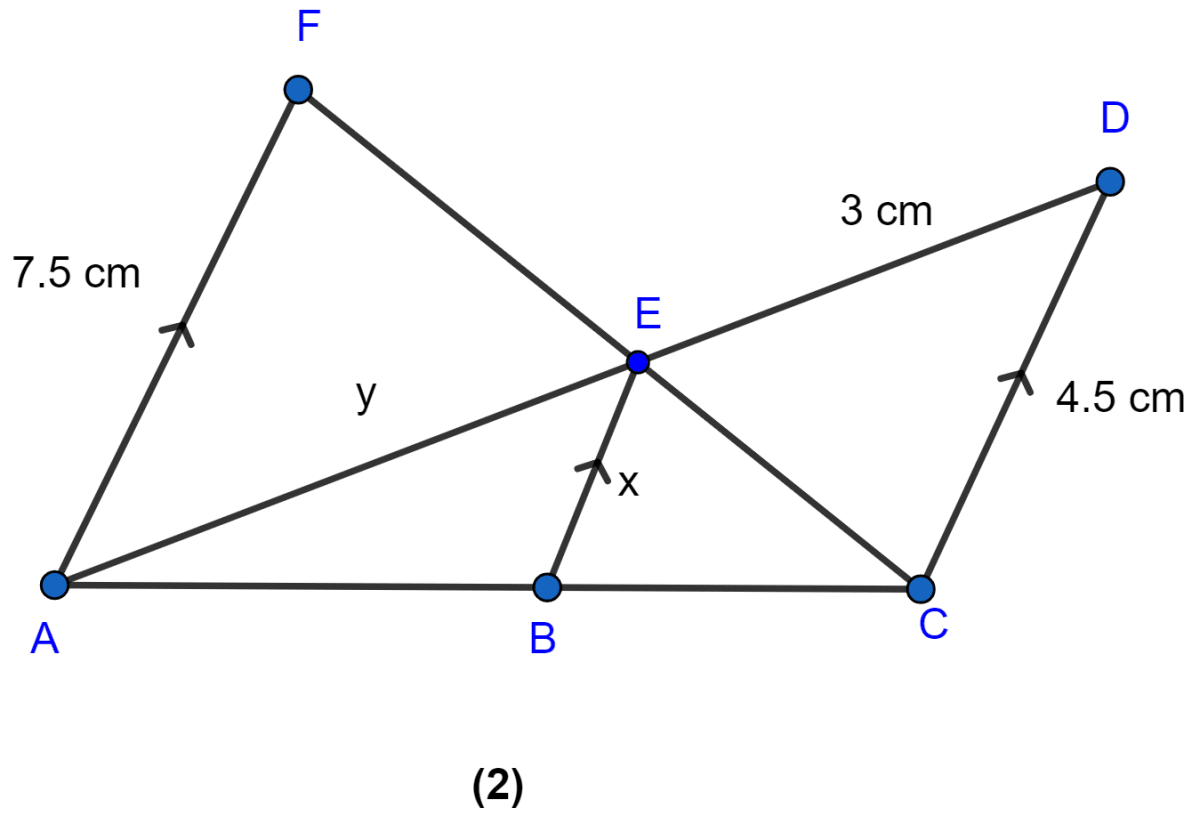
In the figure (2) given below, AF, BE and CD are parallel lines. Given that AF = 7.5 cm, CD = 4.5 cm, ED = 3 cm and BE = x and AE = y. Find the values of x and y.
A 15 meters high tower casts a shadow of 24 metres long at a certain time and at the same time, a telephone pole casts a shadow 16 meters long. Find the height of the telephone pole.
A street light bulb is fixed on a pole 6m above the level of street. If a woman of height 1.5 m casts a shadow of 3 m, find how far she is away from the base of the pole ?