Mathematics
A street light bulb is fixed on a pole 6m above the level of street. If a woman of height 1.5 m casts a shadow of 3 m, find how far she is away from the base of the pole ?
Similarity
20 Likes
Answer
Let AB be the pole and DE be the woman as shown in the figure below:
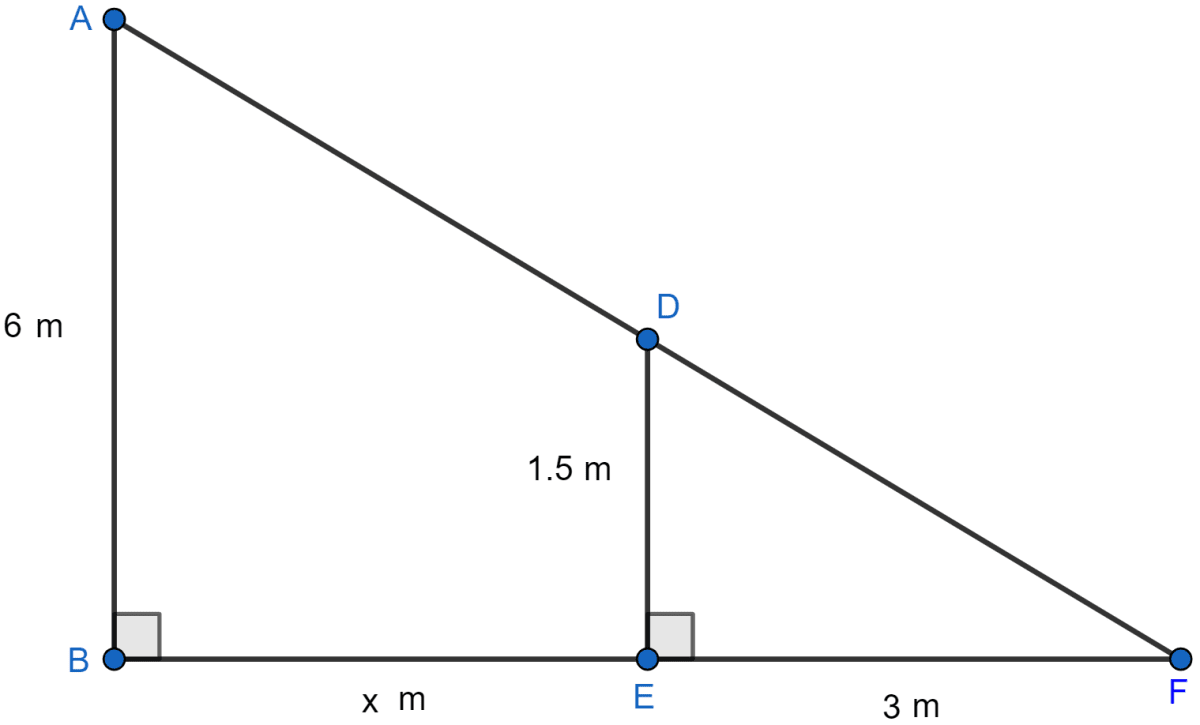
Height of pole (AB) = 6 m
and height of a woman (DE) = 1.5 m
Here shadow EF = 3 m
Let BE(Distance of woman from pole) = x meters.
Considering △ABF and △EFD
∠ABF = ∠DEF (Both are equal to 90°)
∠F = ∠F [Common angles]
So, by AA rule of similarity △ABF ~ △EFD. Hence, the ratio of corresponding sides will be equal.
Hence, woman is 9 m away from the pole.
Answered By
11 Likes
Related Questions
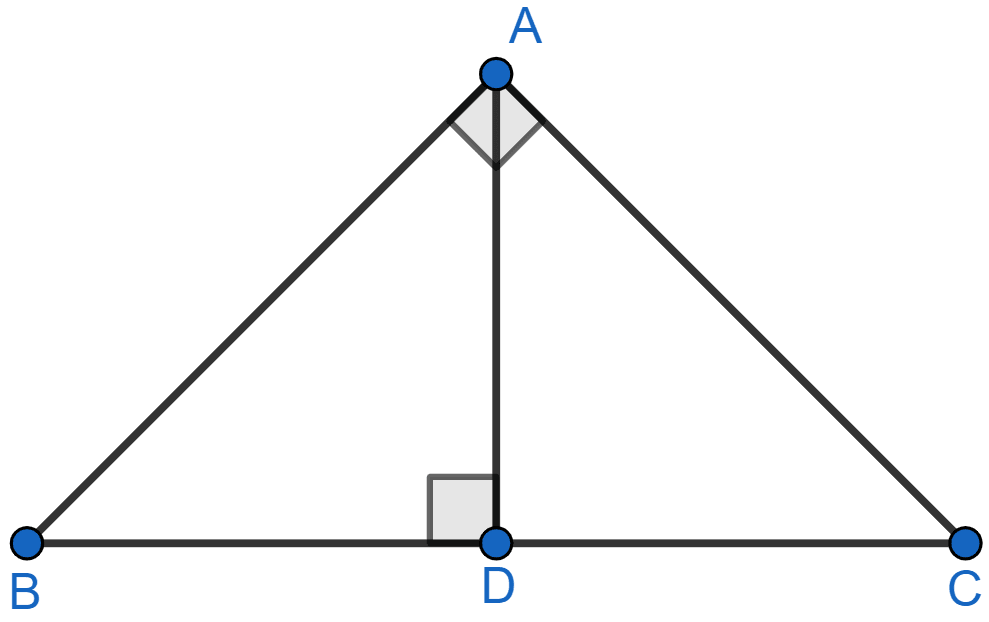
In the given figure, ∠A = 90° and AD ⊥ BC. If BD = 2 cm and CD = 8 cm, find AD.
A 15 meters high tower casts a shadow of 24 metres long at a certain time and at the same time, a telephone pole casts a shadow 16 meters long. Find the height of the telephone pole.
In the figure (i) given below, if DE ∥ BC, AD = 3 cm, BD = 4 cm and BC = 5 cm, find (i) AE : EC (ii) DE.

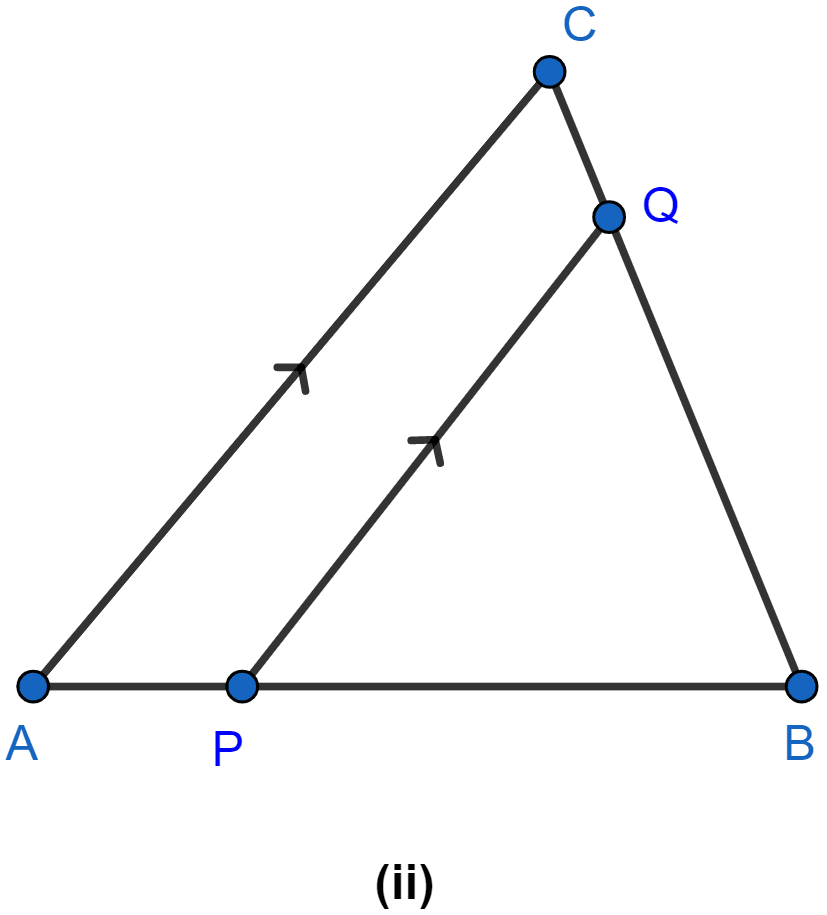
In the figure (ii) given below, PQ ∥ AC, AP = 4 cm, PB = 6 cm and BC = 8 cm, find CQ and BQ.