Mathematics
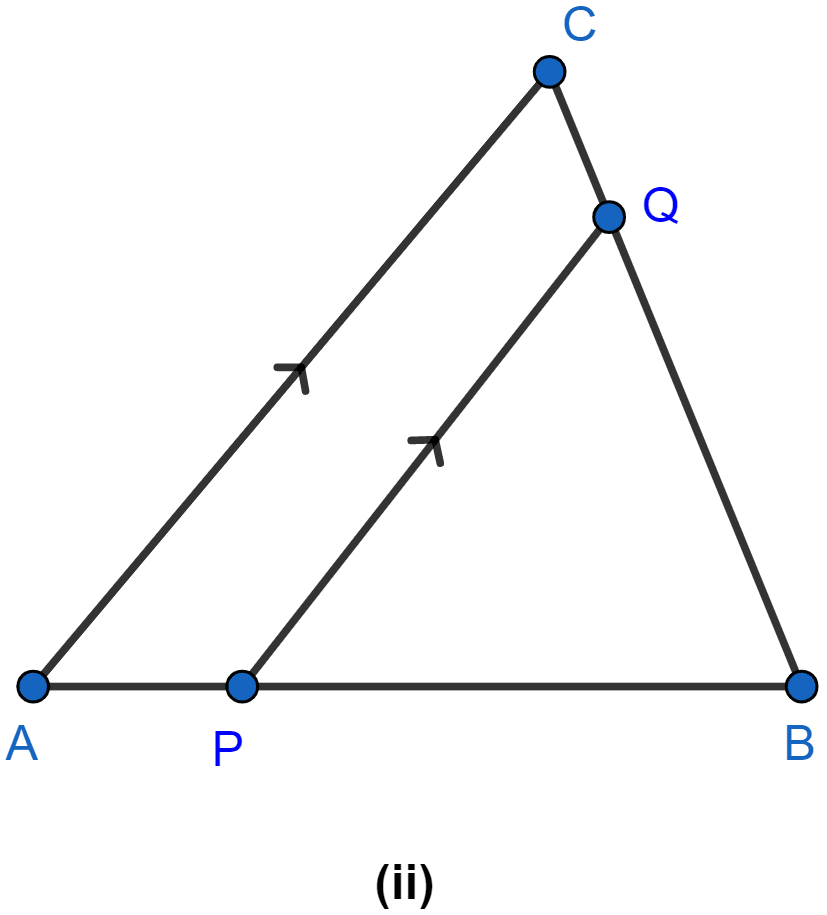
In the figure (ii) given below, PQ ∥ AC, AP = 4 cm, PB = 6 cm and BC = 8 cm, find CQ and BQ.
Similarity
41 Likes
Answer
Considering △ABC and △PBQ,
∠B = ∠B (Common angle)
∠BPQ = ∠BAC (Corresponding angle are equal)
So, by AA rule of similarity △ABC ~ △PBQ.
CQ = BC - BQ = 8 - 4.8 = 3.2 .
Hence, BQ = 4.8 cm and CQ = 3.2 cm.
Answered By
25 Likes
Related Questions
A street light bulb is fixed on a pole 6m above the level of street. If a woman of height 1.5 m casts a shadow of 3 m, find how far she is away from the base of the pole ?
In the figure (i) given below, if DE ∥ BC, AD = 3 cm, BD = 4 cm and BC = 5 cm, find (i) AE : EC (ii) DE.

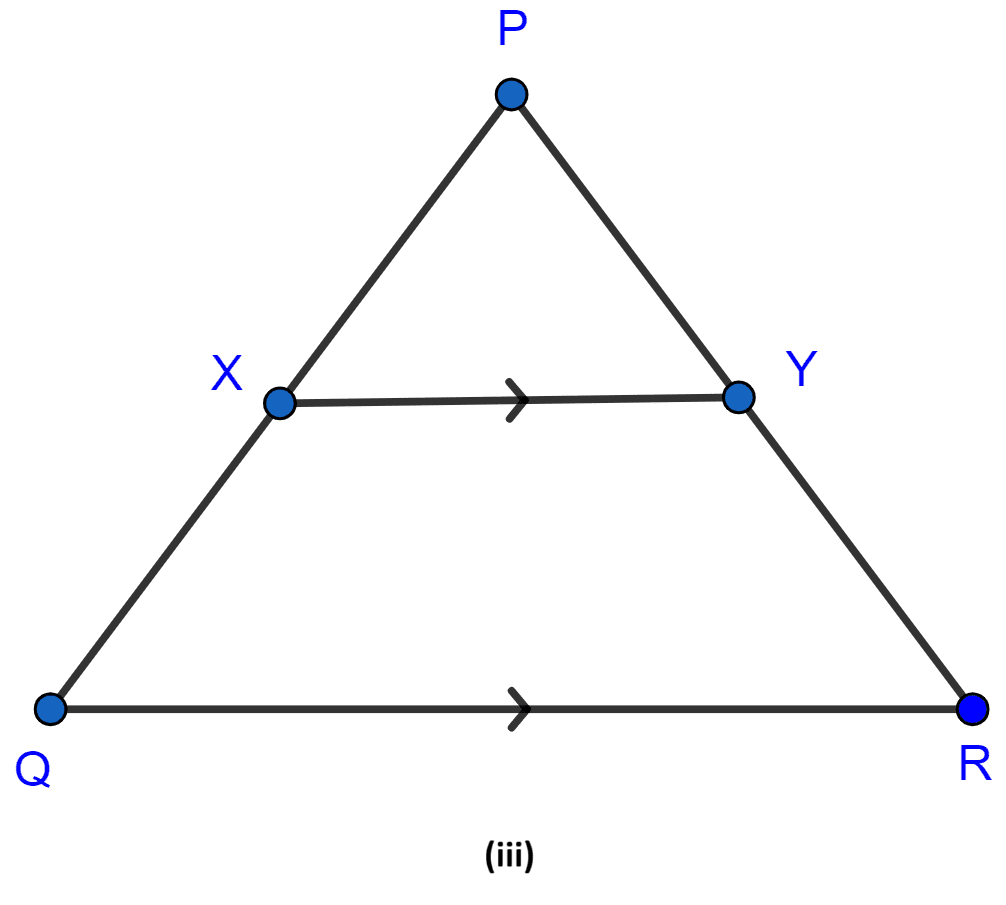
In the figure (iii) given below, if XY ∥ QR, PX = 1 cm, QX = 3 cm, YR = 4.5 cm and QR = 9 cm, find PY and XY.
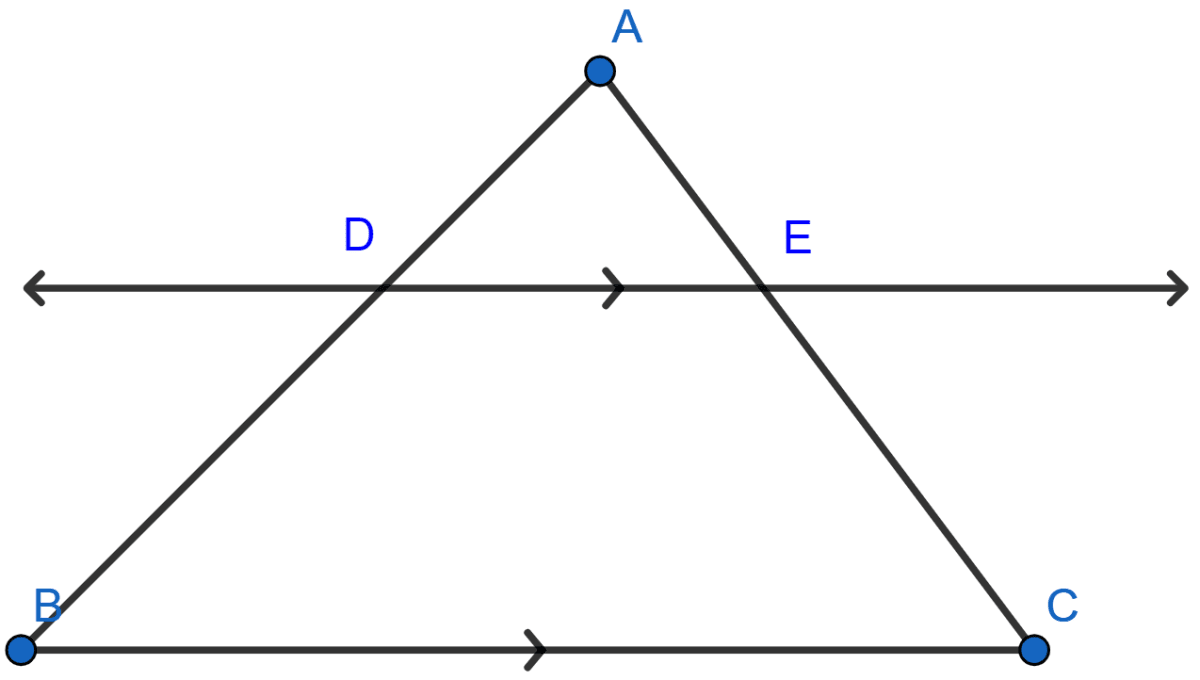
In the adjoining figure, DE ∥ BC.
(i) If AD = x, DB = x - 2, AE = x + 2 and EC = x - 1, find the value of x.
(ii) If DB = x - 3, AB = 2x, EC = x - 2 and AC = 2x + 3, find the value of x.