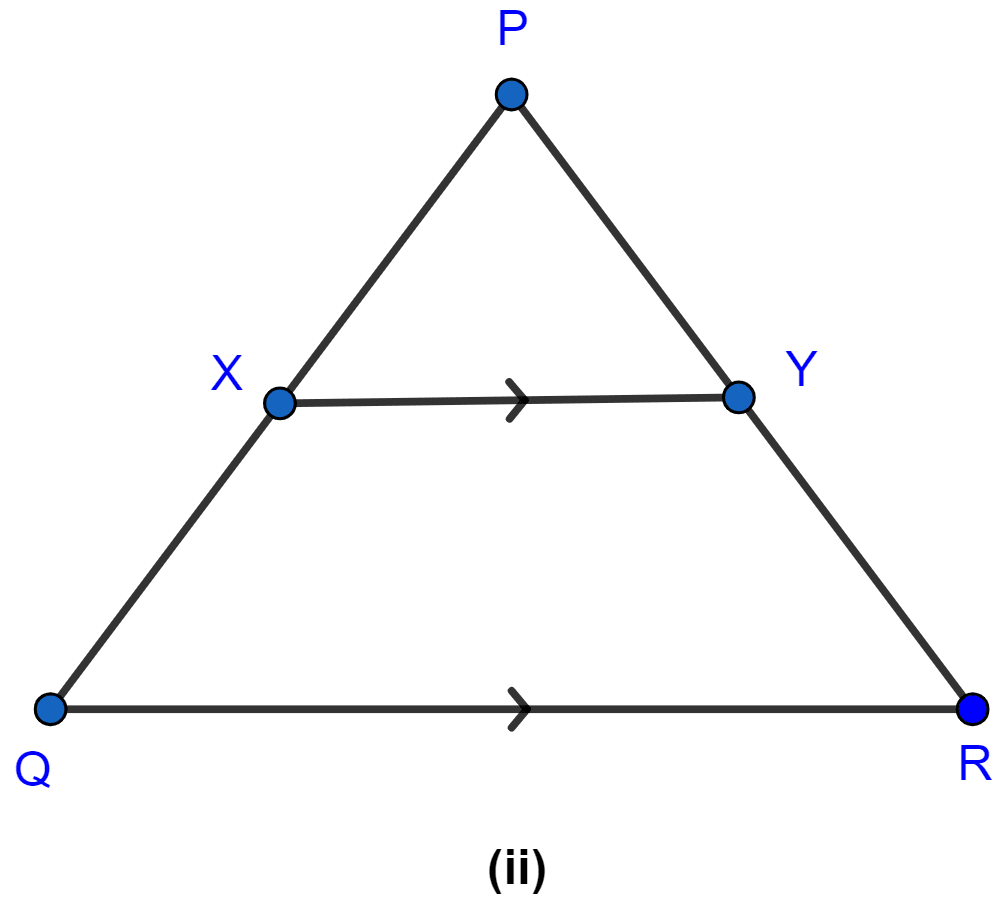
In the figure (iii) given below, if XY ∥ QR, PX = 1 cm, QX = 3 cm, YR = 4.5 cm and QR = 9 cm, find PY and XY.

Considering △PQR and △PXY,

∠P = ∠P (Common angle)
∠PXY = ∠PQR (Corresponding angles)

So, by AA rule of similarity △PQR ~ △PXY. Since ratio of corresponding sides is same,

$\therefore \dfrac{PX}{QX} = \dfrac{PY}{YR} \\[1em] \Rightarrow \dfrac{1}{3} = \dfrac{PY}{4.5} \\[1em] \Rightarrow PY = \dfrac{4.5}{3} \\[1em] \Rightarrow PY = 1.5 \\[1em]$

As triangles are similar so ratio of corresponding sides is same,

$\therefore \dfrac{XY}{QR} = \dfrac{PX}{PQ} \\[1em] \Rightarrow \dfrac{XY}{9} = \dfrac{1}{1 + 3} \\[1em] \Rightarrow XY = \dfrac{9}{4} \\[1em] \Rightarrow XY = 2.25$

Hence, the value of PY = 1.5 cm and XY = 2.25 cm.