Mathematics
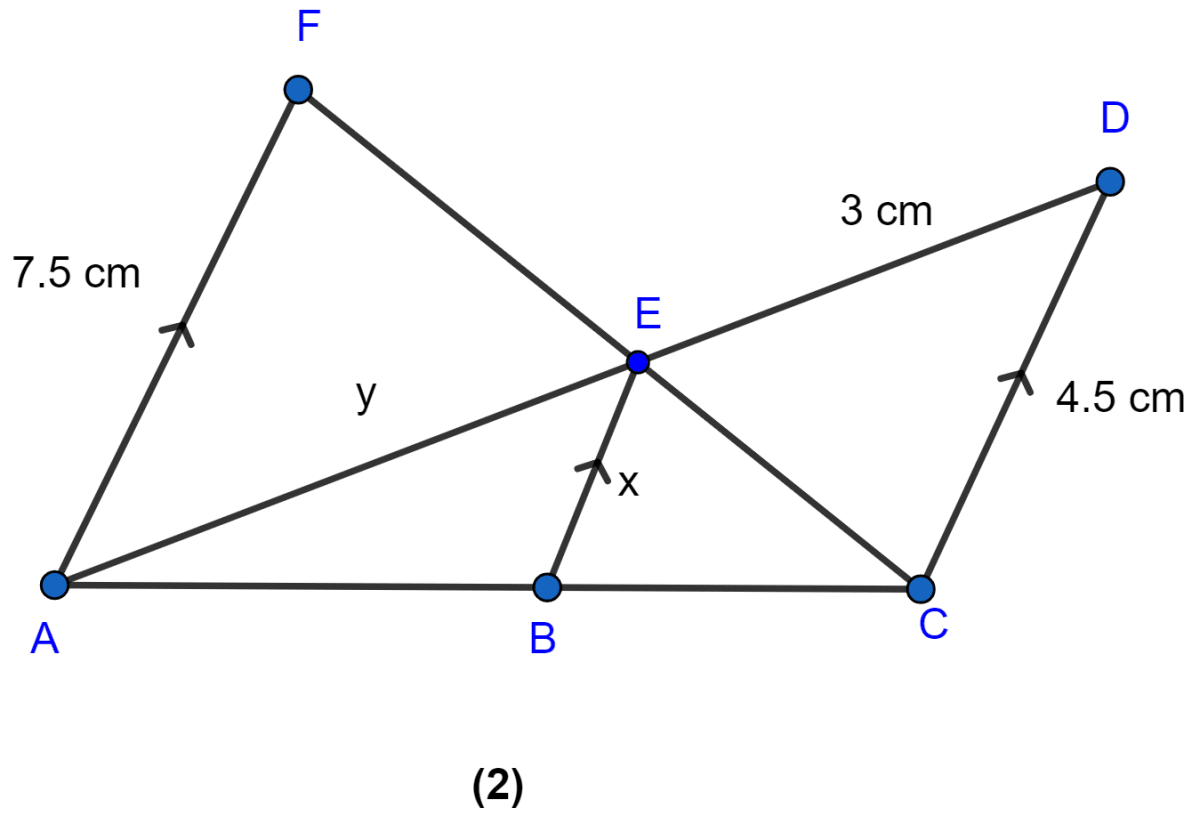
In the figure (2) given below, AF, BE and CD are parallel lines. Given that AF = 7.5 cm, CD = 4.5 cm, ED = 3 cm and BE = x and AE = y. Find the values of x and y.
Similarity
77 Likes
Answer
Consider △AEF and △CED
∠AEF = ∠CED [Vertically opposite angles]
∠F = ∠C [Alternate angles are equal]
So, by AA rule of similarity △AEF ~ △CED
Then,
Consider △ABE and △ACD
∠A = ∠A [Common angles]
∠ABE = ∠ACD [Alternate angles are equal]
So, by AA rule of similarity △ABE ~ △ACD.
Then,
Hence, the value of x = cm and y = 5 cm.
Answered By
42 Likes
Related Questions
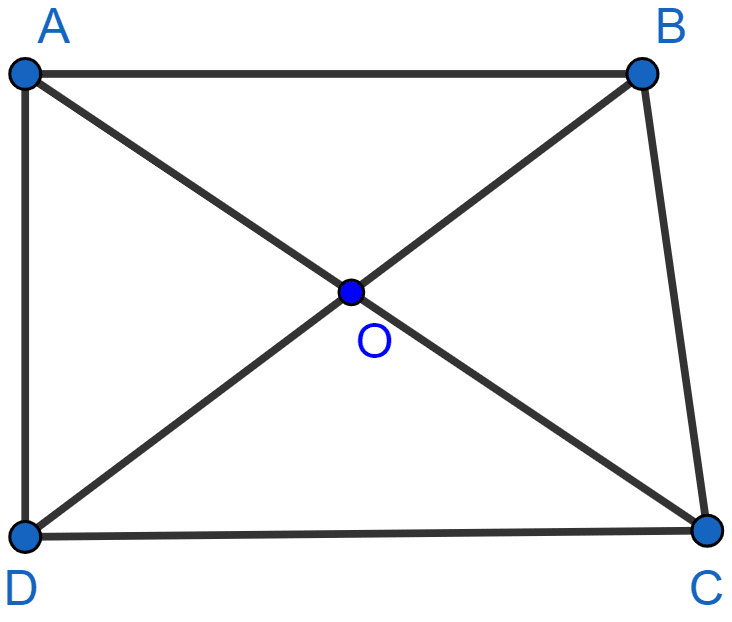
In the adjoining figure, ABCD is a trapezium in which AB ∥ DC. The diagonals AC and BD intersect at O. Prove that
Using the above result, find the value(s) of x if OA = 3x - 19, OB = x - 4, OC = x - 3 and OD = 4.
In the figure (1) given below, AB, EF and CD are parallel lines. Given that AB = 15 cm, EG = 5 cm, GC = 10 cm and DC = 18 cm. Calculate
(i) EF (ii) AC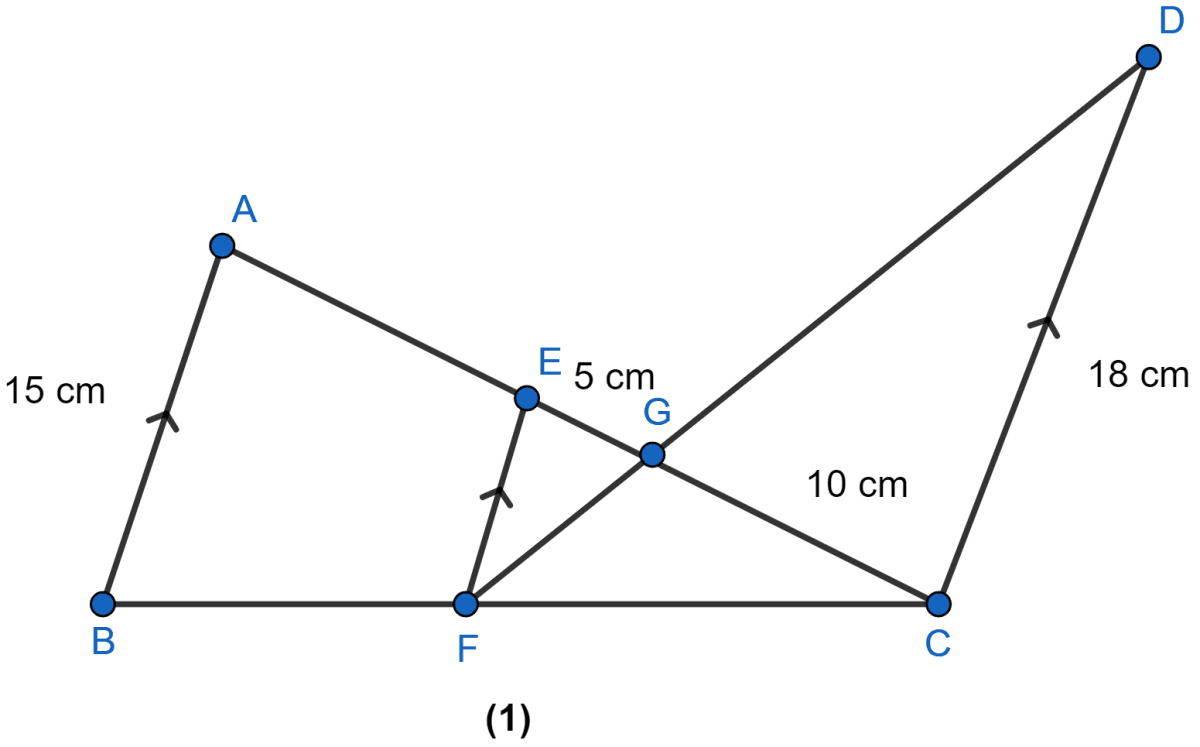
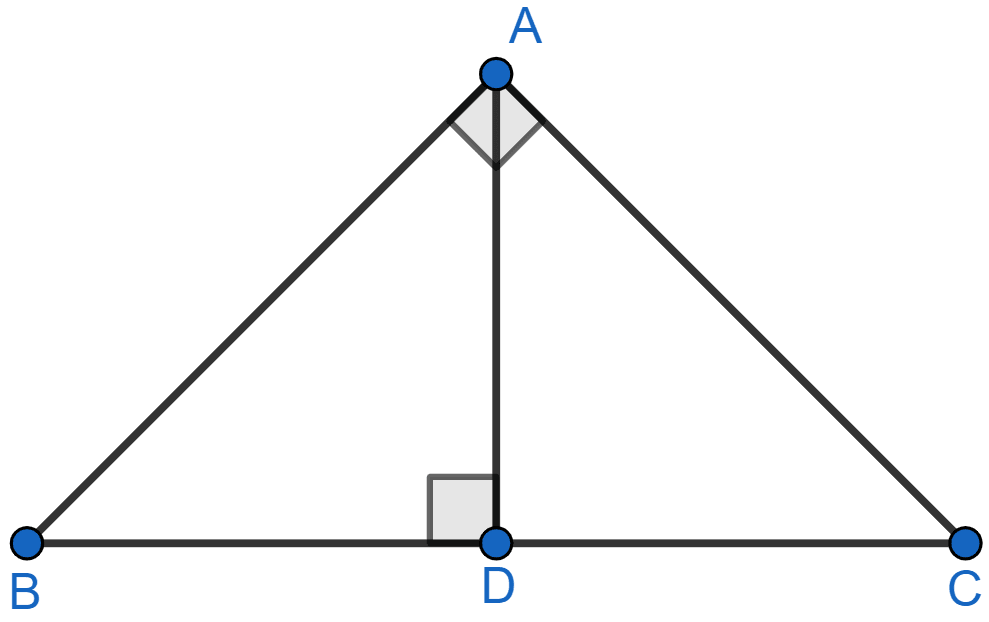
In the given figure, ∠A = 90° and AD ⊥ BC. If BD = 2 cm and CD = 8 cm, find AD.
A 15 meters high tower casts a shadow of 24 metres long at a certain time and at the same time, a telephone pole casts a shadow 16 meters long. Find the height of the telephone pole.