Mathematics
Without using set square or protractor construct :
(i) Triangle ABC, in which AB = 5.5 cm, BC = 3.2 cm and CA = 4.8 cm.
(ii) Draw the locus of a point which moves so that it is always 2.5 cm from B.
(iii) Draw the locus of a point which moves so that it is equidistant from the sides BC and CA.
(iv) Mark the point of intersection of the loci with the letter P and measure PC.
Locus
Answer
(i) Steps of Construction :
Draw BC = 3.2 cm as base.
From B cut an arc of of 5.5 cm and from C cut an arc of 4.8 cm. Take their intersection as point A.
Join the points to form triangle ABC.
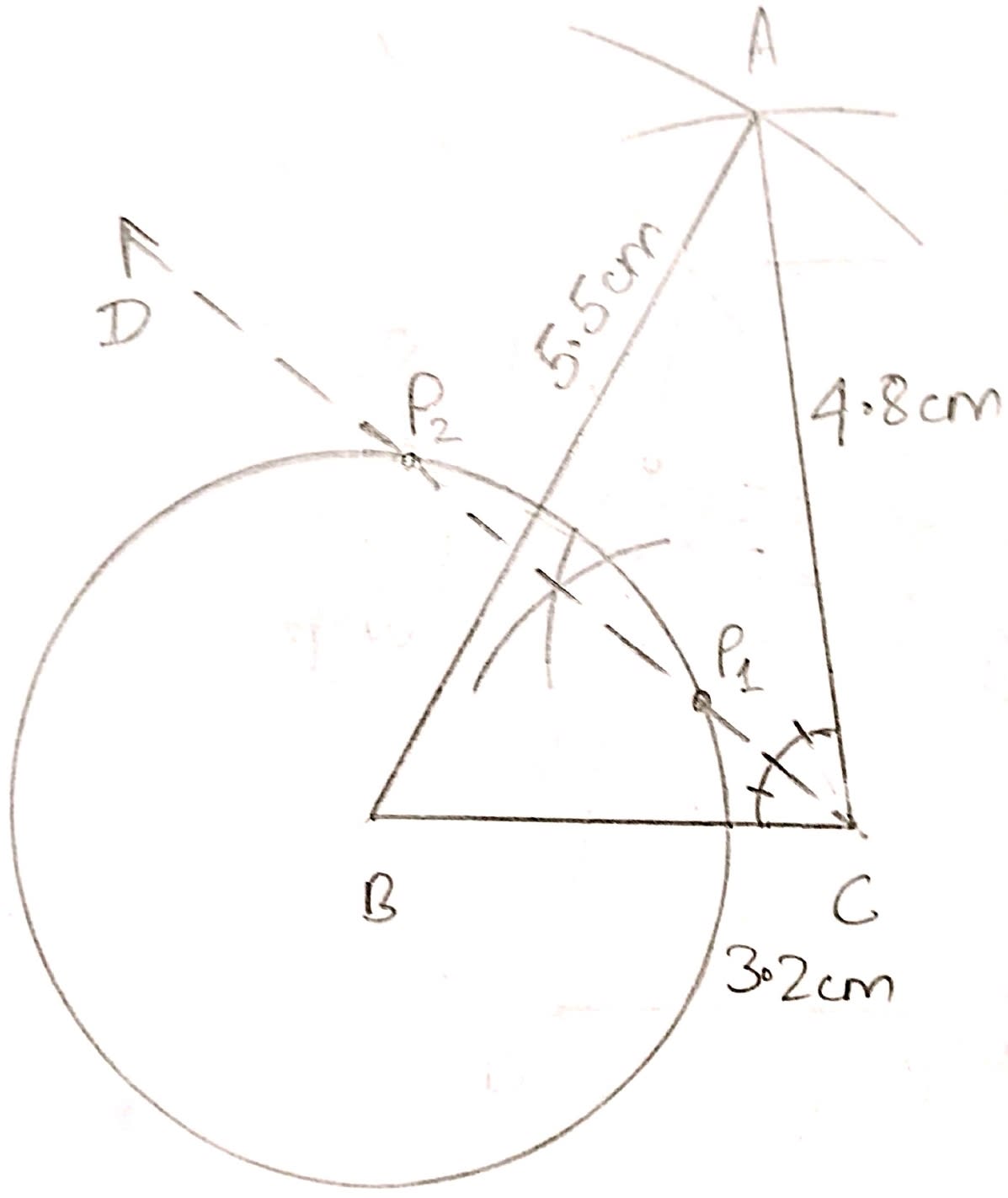
(ii) The locus of point that is always 2.5 cm from point B will be a circle with center as B and radius 2.5 cm.
(iii) We know that locus of points equidistant from two lines is the angle bisector of angle between them.
From figure,
CD is the angular bisectors of ACB, hence it will be equidistant from CA and BC.
(iv) There are two points P1 and P2 which intersect the circle.
On measuring we get,
P1C = 1.1 cm and P2C = 3.6 cm.
Answered By
Related Questions
Without using set square or protractor, construct the quadrilateral ABCD in which ∠BAD = 45°, AD = AB = 6 cm, BC = 3.6 cm and CD = 5 cm.
(i) Measure ∠BCD.
(ii) Locate the point P on BD which is equidistant from BC and CD.
Without using set square or protractor, construct rhombus ABCD with sides of length 4 cm and diagonal AC of length 5 cm. Measure ∠ABC. Find the point R on AD such that RB = RC. Measure the length of AR.
By using ruler and compasses only, construct an isosceles triangle ABC in which BC = 5 cm, AB = AC and ∠BAC = 90°. Locate the point P such that
(i) P is equidistant from the sides BC and AC.
(ii) P is equidistant from the points B and C.
Using ruler and compass only, construct a semicircle with diameter BC = 7 cm. Locate a point P on the circumference of the semicircle such that A is equidistant from B and C. Completely the cyclic quadrilateral ABCD such that D is equidistant from AB and BC. Measure ∠ADC and write it down.