Mathematics
Using ruler and compass only, construct a semicircle with diameter BC = 7 cm. Locate a point P on the circumference of the semicircle such that A is equidistant from B and C. Completely the cyclic quadrilateral ABCD such that D is equidistant from AB and BC. Measure ∠ADC and write it down.
Locus
24 Likes
Answer
Steps of construction :
Draw a line segment BC = 7 cm.
Create a semicircle with BC as diameter.
Make right bisector of BC and construct perpendicular from it such that it meets the semicircle at A as shown in figure.
Construct angle bisector of ∠ABC, and let it meet the semicircle at point D.
Join the points to form quadrilateral ABCD.
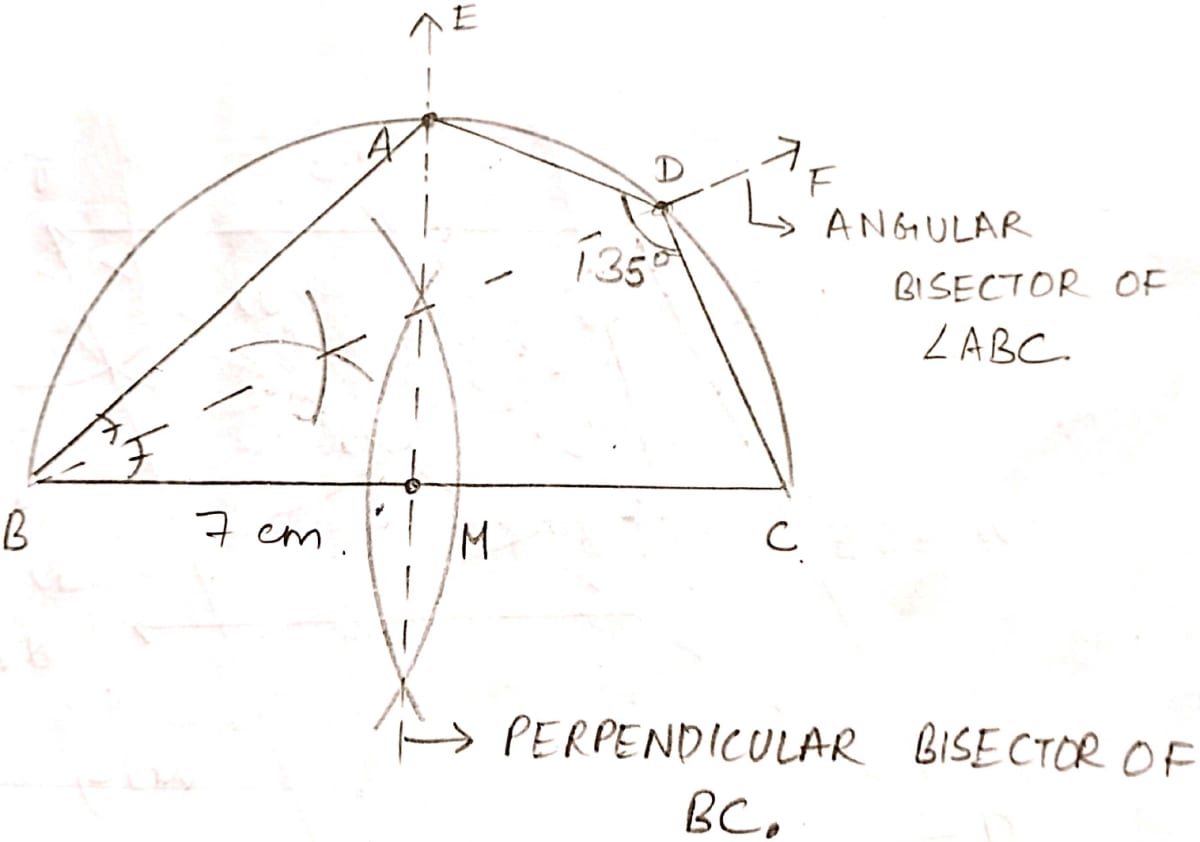
On, measuring we get ∠ADC = 135°.
Answered By
15 Likes
Related Questions
Using ruler and compasses only, construct a quadrilateral ABCD in which AB = 6 cm, BC = 5 cm, ∠B = 60°, AD = 5 cm and D is equidistant from AB and BC. Measure CD.
By using ruler and compasses only, construct an isosceles triangle ABC in which BC = 5 cm, AB = AC and ∠BAC = 90°. Locate the point P such that
(i) P is equidistant from the sides BC and AC.
(ii) P is equidistant from the points B and C.
Construct an isosceles triangle ABC such that AB = 6 cm, BC = AC = 4 cm. Bisect ∠C internally and mark a point P on this bisector such that CP = 5 cm. Find the points Q and R which are 5 cm from P and also 5 cm from the line AB.
Without using set square or protractor construct :
(i) Triangle ABC, in which AB = 5.5 cm, BC = 3.2 cm and CA = 4.8 cm.
(ii) Draw the locus of a point which moves so that it is always 2.5 cm from B.
(iii) Draw the locus of a point which moves so that it is equidistant from the sides BC and CA.
(iv) Mark the point of intersection of the loci with the letter P and measure PC.