Mathematics
Using a graph paper, draw an ogive for the following distribution which shows a record of the weight in kilograms of 200 students.
| Weight | Frequency |
|---|---|
| 40 - 45 | 5 |
| 45 - 50 | 17 |
| 50 - 55 | 22 |
| 55 - 60 | 45 |
| 60 - 65 | 51 |
| 65 - 70 | 31 |
| 70 - 75 | 20 |
| 75 - 80 | 9 |
Use your ogive to estimate the following :
(i) The percentage of students weighing 55 kg or more.
(ii) The weight above which the heaviest 30% of the students fall,
(iii) The number of students who are (a) under-weight and (b) over weight, if 55.70 kg is considered as standard weight ?
Measures of Central Tendency
37 Likes
Answer
(i) Cumulative frequency distribution table :
| Weight | Frequency | Cumulative frequency |
|---|---|---|
| 40 - 45 | 5 | 5 |
| 45 - 50 | 17 | 22 (5 + 17) |
| 50 - 55 | 22 | 44 (22 + 22) |
| 55 - 60 | 45 | 89 (44 + 45) |
| 60 - 65 | 51 | 140 (89 + 51) |
| 65 - 70 | 31 | 171 (140 + 31) |
| 70 - 75 | 20 | 191 (171 + 20) |
| 75 - 80 | 9 | 200 (191 + 9) |
Steps of construction :
Since, the scale on x-axis starts at 40, a break (kink) is shown near the origin on x-axis to indicate that the graph is drawn to scale beginning at 40.
Take 1 cm along x-axis = 5 kg.
Take 1 cm along y-axis = 20 units.
Plot the point (40, 0) as ogive starts from x-axis representing lower limit of first class.
Plot the points (45, 5), (50, 22), (55, 44), (60, 89), (65, 140), (70, 171), (75, 191) and (80, 200).
Join the points by a free hand curve.
Draw a line parallel to y-axis from point J (weight) = 55, touching the graph at point Q. From point Q draw a line parallel to x-axis touching y-axis at point K.
From graph, K = 44.
Hence, 44 students weight 55 kg or less.
Students weighing more than 55 kg = 200 - 44 = 156.
Percentage of students weighing more than 55 kg = = 78%.
Hence, percentage of students weighing more than 55 kg = 78%.
(ii) 30% of students = = 60.
Total students = 200
No. of Students not in heaviest 30% = 200 - 60 = 140.
Draw a line parallel to x-axis from point O (no. of students) = 140, touching the graph at point R. From point R draw a line parallel to y-axis touching x-axis at point P.
From graph, P = 65
Hence, above 65 kg the heaviest 30% of the students fall.
(iii) Draw a line parallel to y-axis from point L (weight) = 55.70 kg, touching the graph at point M. From point M draw a line parallel to x-axis touching y-axis at point N.
(a) From graph,
N = 46.
∴ 46 students have weight less than 55.70 kg
Hence, 46 students are underweight.
(b) Since, 46 students have weight less than 55.70 kg
∴ 154 (200 - 46) students have weight more than 55.70 kg
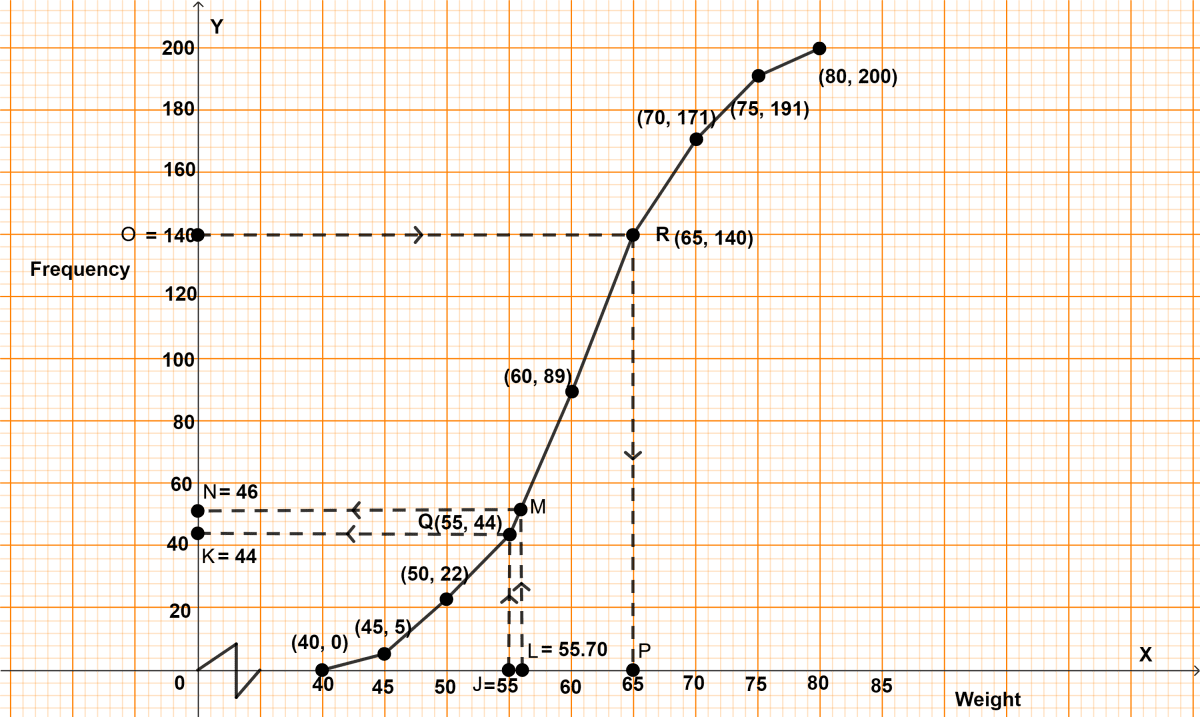
Hence, 154 students are overweight.
Answered By
14 Likes
Related Questions
In a malaria epidemic, the number of cases diagnosed were as follows :
Date (July) Number 1 5 2 12 3 20 4 27 5 46 6 30 7 31 8 18 9 11 10 5 11 0 12 1 On what days do the mode, the upper and the lower quartiles occur ?
The marks obtained by 120 students in a Mathematics test are given below :
Marks No. of students 0 - 10 5 10 - 20 9 20 - 30 16 30 - 40 22 40 - 50 26 50 - 60 18 60 - 70 11 70 - 80 6 80 - 90 4 90 - 100 3 Draw an ogive for the given distribution on a graph sheet. Use a suitable scale for your ogive. Use your ogive to estimate :
(i) the median
(ii) the number of students who obtained more than 75% marks in a test ?
(iii) the number of students who did not pass in the test if the pass percentage was 40?
(iv) the lower quartile.
The distribution given below, shows the marks obtained by 25 students in an aptitude test. Find the mean, median and mode of the distribution.
Marks obtained No. of students 5 3 6 9 7 6 8 4 9 2 10 1 The monthly income of a group of 320 employees in a company is given below :
Monthly income No. of employees 6 - 7 20 7 - 8 45 8 - 9 65 9 - 10 95 10 - 11 60 11 - 12 30 12 - 13 5 Draw an ogive of the given distribution on a graph sheet taking 2 cm = ₹ 1000 on one axis and 2 cm = 50 employees on the other axis. From the graph determine :
(i) the median wage.
(ii) the number of employees whose income is below ₹ 8500.
(iii) if the salary of a senior employee is above ₹ 11500, find the number of senior employees in the company.
(iv) the upper quartile.