Mathematics
The monthly income of a group of 320 employees in a company is given below :
| Monthly income | No. of employees |
|---|---|
| 6 - 7 | 20 |
| 7 - 8 | 45 |
| 8 - 9 | 65 |
| 9 - 10 | 95 |
| 10 - 11 | 60 |
| 11 - 12 | 30 |
| 12 - 13 | 5 |
Draw an ogive of the given distribution on a graph sheet taking 2 cm = ₹ 1000 on one axis and 2 cm = 50 employees on the other axis. From the graph determine :
(i) the median wage.
(ii) the number of employees whose income is below ₹ 8500.
(iii) if the salary of a senior employee is above ₹ 11500, find the number of senior employees in the company.
(iv) the upper quartile.
Measures of Central Tendency
15 Likes
Answer
(i) Cumulative frequency distribution table :
| Monthly income | No. of employees | Cumulative frequency |
|---|---|---|
| 6 - 7 | 20 | 20 |
| 7 - 8 | 45 | 65 (20 + 45) |
| 8 - 9 | 65 | 130 (65 + 65) |
| 9 - 10 | 95 | 225 (130 + 95) |
| 10 - 11 | 60 | 285 (225 + 60) |
| 11 - 12 | 30 | 315 (285 + 30) |
| 12 - 13 | 5 | 320 (315 + 5) |
Here, n = 320, which is even.
By formula,
Median = th term
= = 160th term.
Steps of construction :
Since, the scale on x-axis starts at 6, a break (kink) is shown near the origin on x-axis to indicate that the graph is drawn to scale beginning at 6.
Take 2 cm along x-axis = 1 thousand rupees.
Take 1 cm along y-axis = 40 employees.
Plot the point (6, 0) as ogive starts from x-axis representing lower limit of first class.
Plot the points (7, 20), (8, 65), (9, 130), (10, 225), (11, 285), (12, 315) and (13, 320).
Join the points by a free hand curve.
Draw a line parallel to x-axis from point M (no. of employees) = 160, touching the graph at point N. From point N draw a line parallel to y-axis touching x-axis at point O.
From graph, O = 9.2 (thousands)
Hence, median = ₹ 9200.
(ii) Draw a line parallel to y-axis from point P (income) = ₹ 8.5 (thousands), touching the graph at point Q. From point Q draw a line parallel to x-axis touching y-axis at point R.
From graph, R = 95.
Hence, 95 employees have income less than ₹ 8500.
(iii) Draw a line parallel to y-axis from point S (income) = ₹ 11.5 (thousands), touching the graph at point T. From point T draw a line parallel to x-axis touching y-axis at point U.
From graph, U = 305.
∴ 305 employees have salary less than ₹ 11500.
∴ 15 (320 - 305) employees have salary more than ₹ 11500.
Hence, there are 15 senior employees.
(iv) Here, n = 320, which is even.
By formula,
Upper quartile = = 240th term.
Draw a line parallel to x-axis from point V (no. of employees) = 240, touching the graph at point W. From point W draw a line parallel to y-axis touching x-axis at point Z.
From graph, Z = 10.3 (thousands)
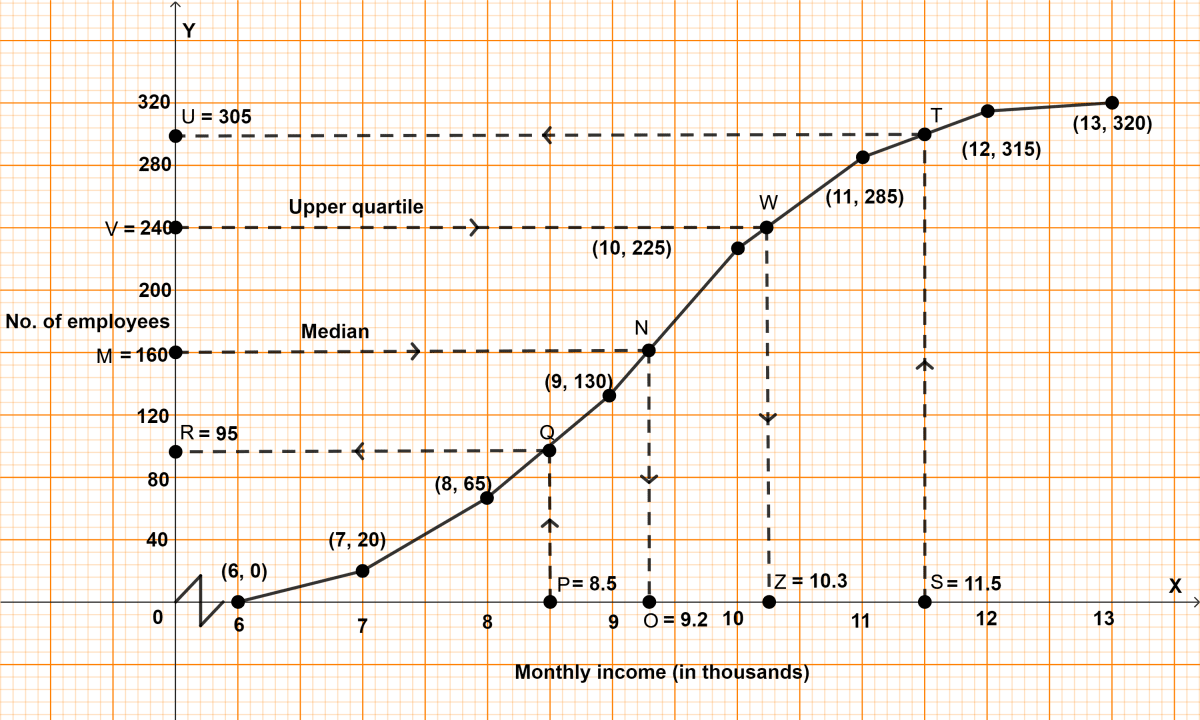
Hence, upper quartile = ₹ 10300.
Answered By
9 Likes
Related Questions
Using a graph paper, draw an ogive for the following distribution which shows a record of the weight in kilograms of 200 students.
Weight Frequency 40 - 45 5 45 - 50 17 50 - 55 22 55 - 60 45 60 - 65 51 65 - 70 31 70 - 75 20 75 - 80 9 Use your ogive to estimate the following :
(i) The percentage of students weighing 55 kg or more.
(ii) The weight above which the heaviest 30% of the students fall,
(iii) The number of students who are (a) under-weight and (b) over weight, if 55.70 kg is considered as standard weight ?
The distribution given below, shows the marks obtained by 25 students in an aptitude test. Find the mean, median and mode of the distribution.
Marks obtained No. of students 5 3 6 9 7 6 8 4 9 2 10 1 The median of the observations 11, 12, 14, (x - 2), (x + 4), (x + 9), 32, 38, 47 are arranged in ascending order is 24. Find the value of x and hence find the mean.
The numbers 6, 8, 10, 12, 13 and x are arranged in an ascending order. If the mean of the observations is equal to the median, find the value of x.