Mathematics
Use ruler and compasses for this question.
(i) Construct an isosceles triangle ABC in which AB = AC = 7.5 cm and BC = 6 cm.
(ii) Draw AD, the perpendicular from vertex A to side BC.
(iii) Draw a circle with center A and radius 2.8 cm, cutting AD at E.
(iv) Construct another circle to circumscribe the triangle BCE.
Constructions
2 Likes
Answer
Steps of construction :
Draw a line BC = 6 cm.
Draw two arc intersecting each other at A having radius 7.5 cm and centre B and C.
Join AC and AB.
Draw perpendicular bisector of BC as AD.
With centre A and radius 2.8 cm, draw a circle which intersects AD at E.
Join EB and EC and draw perpendicular bisector of EB intersecting AD at O.
With centre O and radius OE or OB or OC draw a circle which passes through B and C and touches the first circle at E externally.
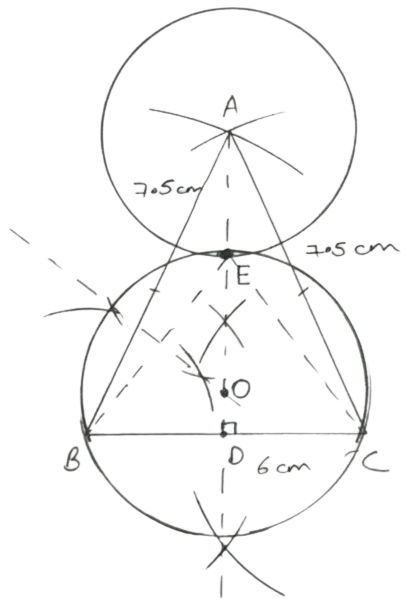
Hence, above is the required circle.
Answered By
1 Like
Related Questions
In triangle ABC, ∠BAC = 90°, AB = 6 cm and BC = 10 cm. A circle is drawn inside the triangle which touches all the sides of the triangle (i.e. an incircle of △ABC is drawn). Find the area of the triangle excluding the circle.
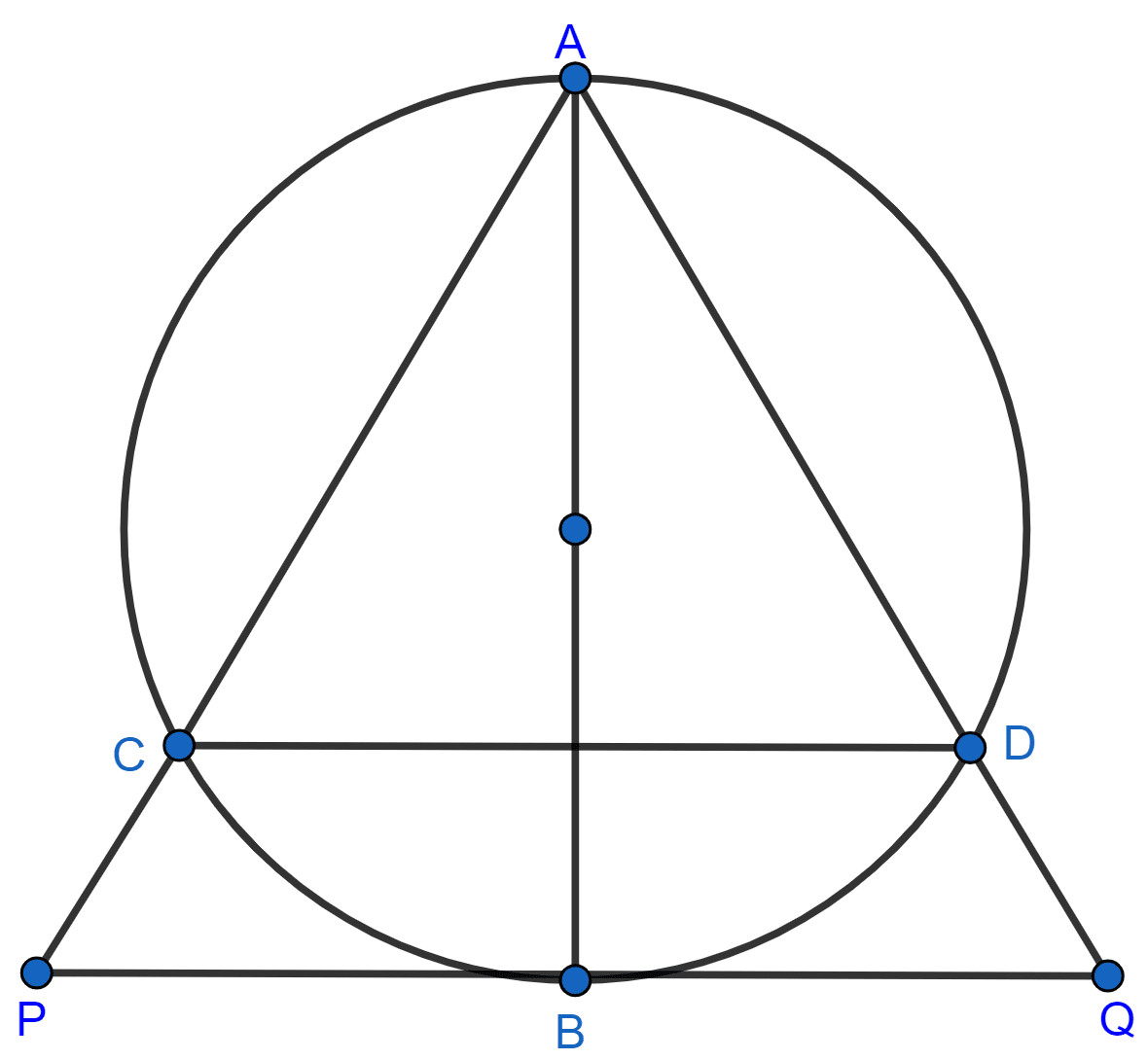
In the given figure, AB is a diameter of the circle. Chords AC and AD produced meet the tangent to the circle at point B in points P and Q respectively. Prove that :
AB2 = AC × AP
A conical vessel of radius 6 cm and height 8 cm is completely filled with water. A sphere is lowered into the water and its size is such that when it touches the sides it is just immersed . What fraction of water overflows ?
In a rectangle ABCD, its diagonal AC = 15 cm and ∠ACD = α. If cot α = , find the perimeter and the area of the rectangle.