Mathematics
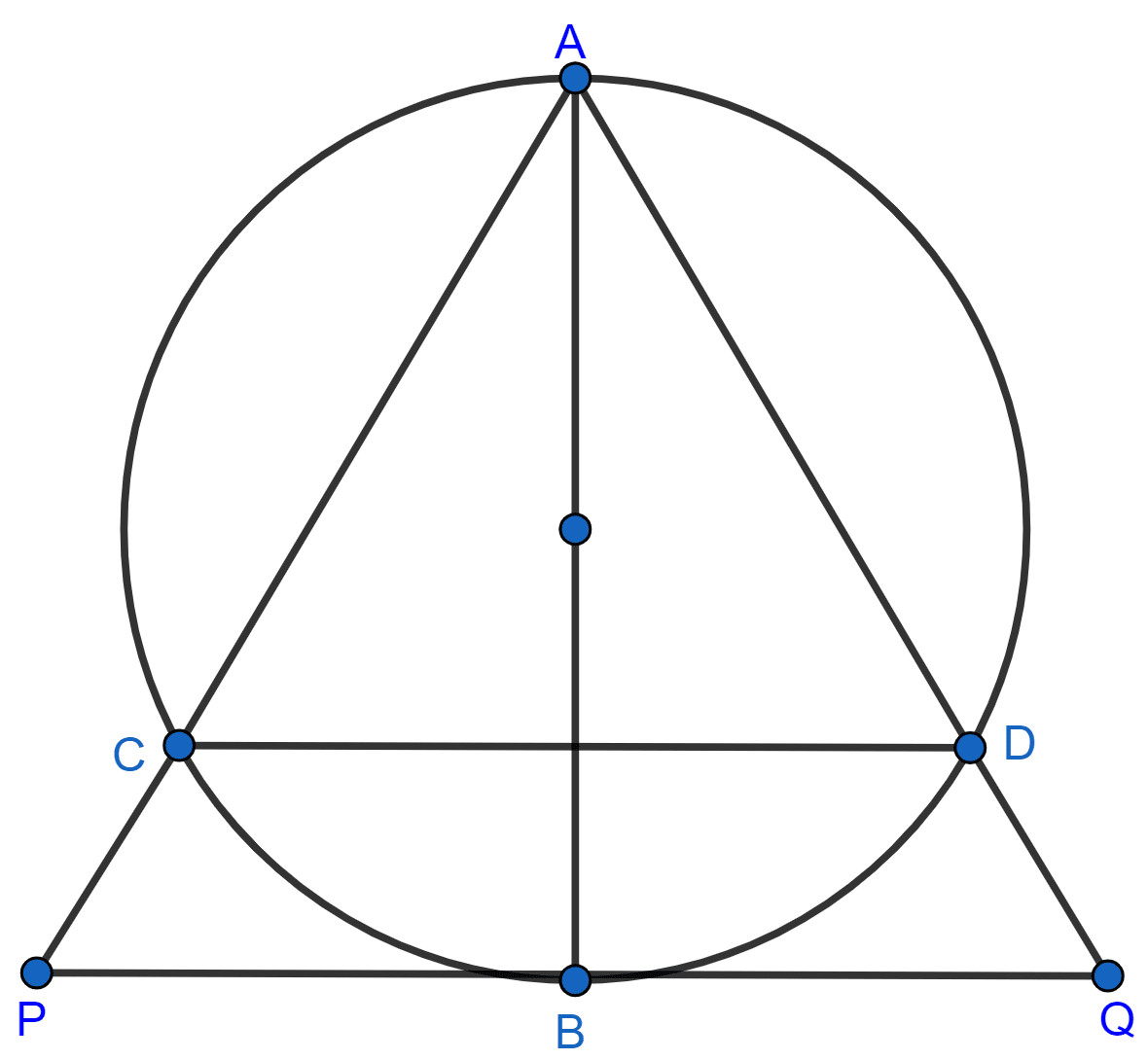
In the given figure, AB is a diameter of the circle. Chords AC and AD produced meet the tangent to the circle at point B in points P and Q respectively. Prove that :
AB2 = AC × AP
Circles
8 Likes
Answer
Join BC.
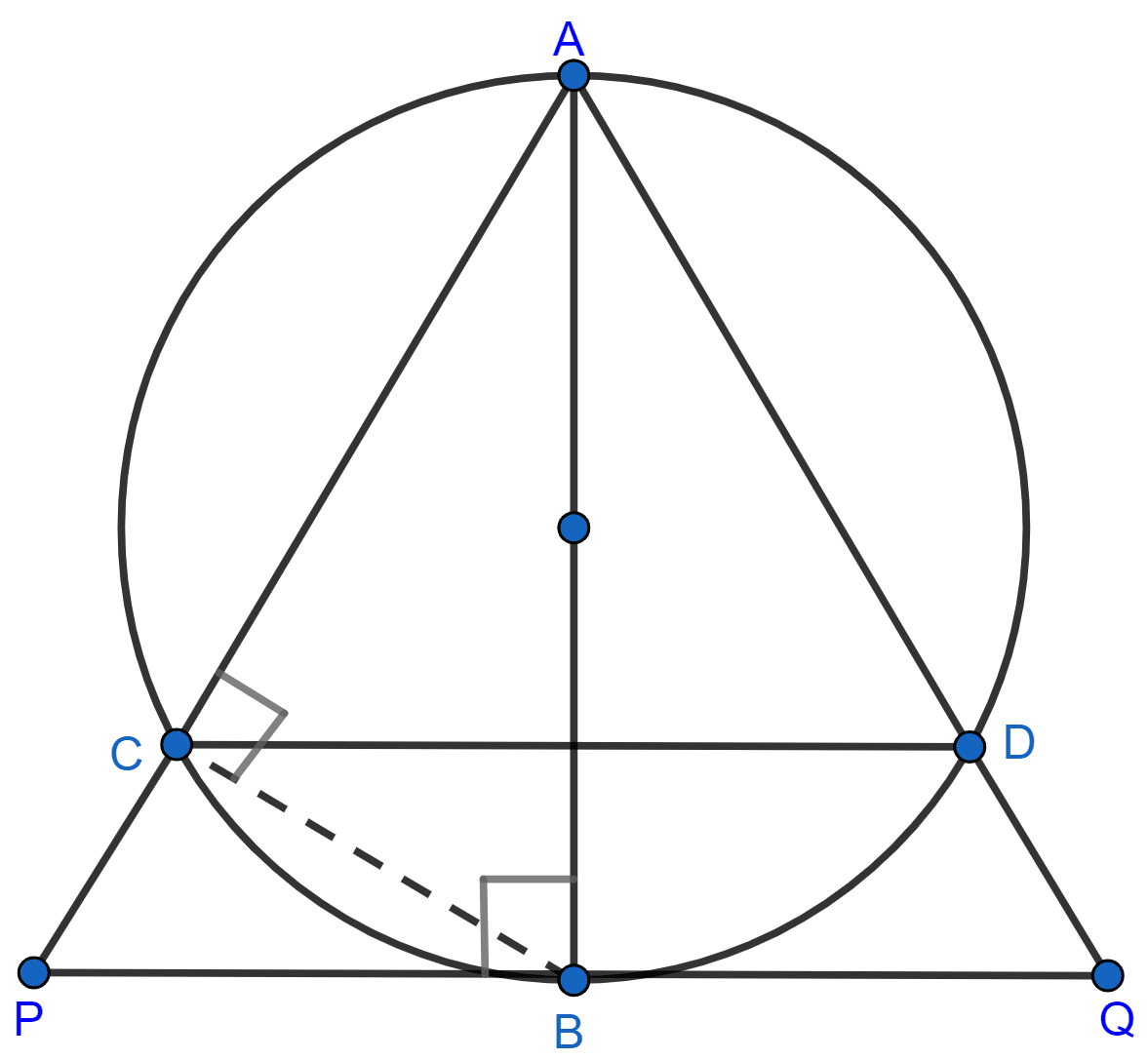
We know that,
The diameter of a circle subtends an angle of 90° at any point on circle.
∴ ∠ACB = 90°
We know that,
A tangent line is perpendicular to the radius line from the center to the point of contact
∴ ∠ABP = 90°
In △ACB and △ABP,
∠ACB = ∠ABP = 90°
∠A = ∠A [Common]
∴ △ACB ~ △ABP [By A.A. axiom]
We know that :
Ratio of corresponding sides of similar triangle are proportional.
⇒ AB2 = AC × AP
Hence, proved that AB2 = AC × AP.
Answered By
6 Likes
Related Questions
In a triangle PQR, L and M are two points on the base QR, such that ∠LPQ = ∠QRP and ∠RPM = ∠RQP. Prove that :
(i) △PQL ~ △RPM
(ii) QL × RM = PL × PM
(iii) PQ2 = QR × QL
In a rectangle ABCD, its diagonal AC = 15 cm and ∠ACD = α. If cot α = , find the perimeter and the area of the rectangle.
Use ruler and compasses for this question.
(i) Construct an isosceles triangle ABC in which AB = AC = 7.5 cm and BC = 6 cm.
(ii) Draw AD, the perpendicular from vertex A to side BC.
(iii) Draw a circle with center A and radius 2.8 cm, cutting AD at E.
(iv) Construct another circle to circumscribe the triangle BCE.
In triangle ABC, ∠BAC = 90°, AB = 6 cm and BC = 10 cm. A circle is drawn inside the triangle which touches all the sides of the triangle (i.e. an incircle of △ABC is drawn). Find the area of the triangle excluding the circle.