Mathematics
In triangle ABC, ∠BAC = 90°, AB = 6 cm and BC = 10 cm. A circle is drawn inside the triangle which touches all the sides of the triangle (i.e. an incircle of △ABC is drawn). Find the area of the triangle excluding the circle.
Circles
4 Likes
Answer
△ABC is shown in the figure below:
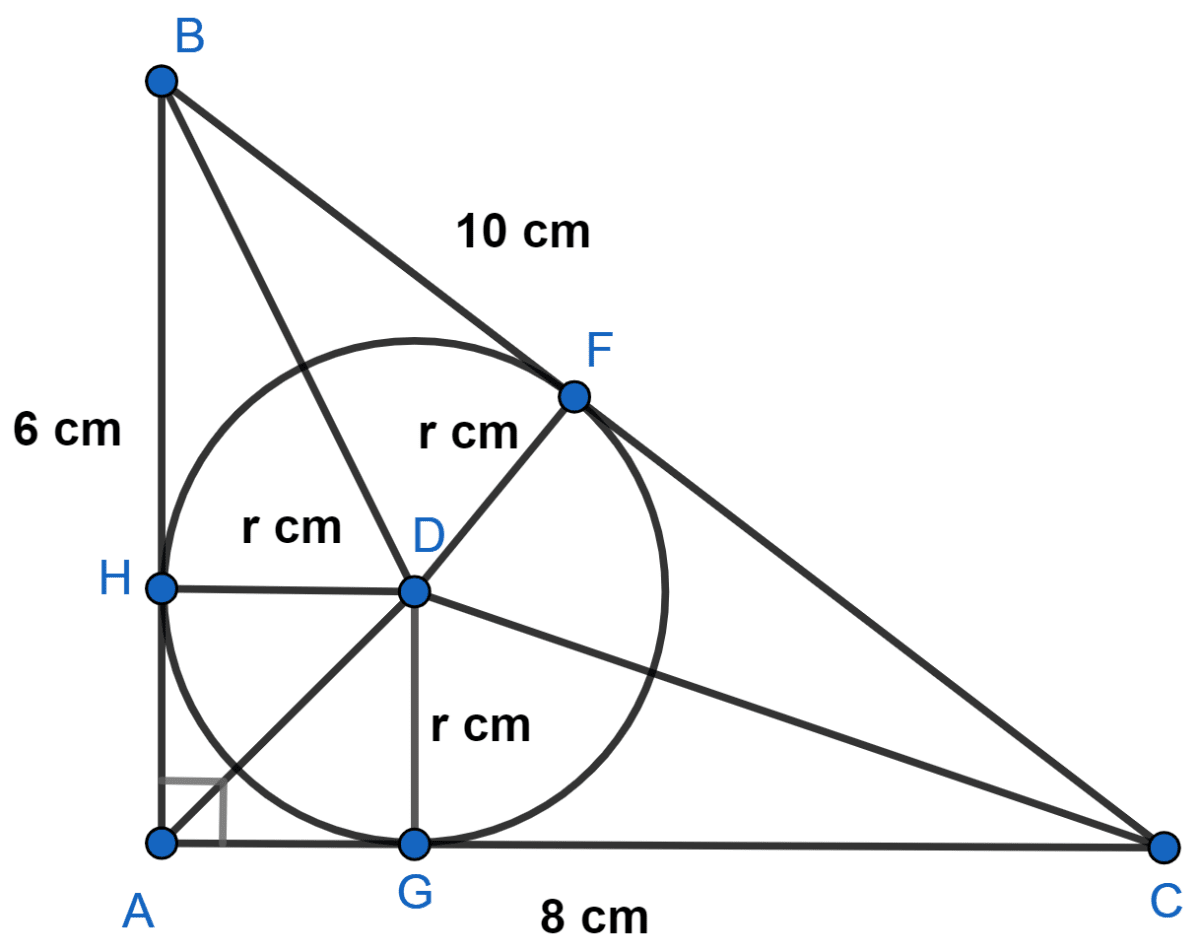
In △ABC,
By pythagoras theorem,
⇒ BC2 = AB2 + AC2
⇒ 102 = 62 + AC2
⇒ AC2 = 100 - 36
⇒ AC2 = 64
⇒ AC = = 8 cm.
A tangent line is perpendicular to the radius line from the center to the point of contact
∴ DF ⊥ BC, DG ⊥ AC and DH ⊥ AB.
Let radius of circle be r.
∴ DF = DG = DH = r
By formula,
Area of triangle = base × height
From figure,
Area of △ABC = Area of △ADC + Area of △CDB + Area of △ADB
Area of triangle (excluding circle) = Area of triangle - Area of circle
= - πr2
= × (2)2
= 24 -
=
=
= cm2.
Hence, area of triangle excluding circle = cm2.
Answered By
2 Likes
Related Questions
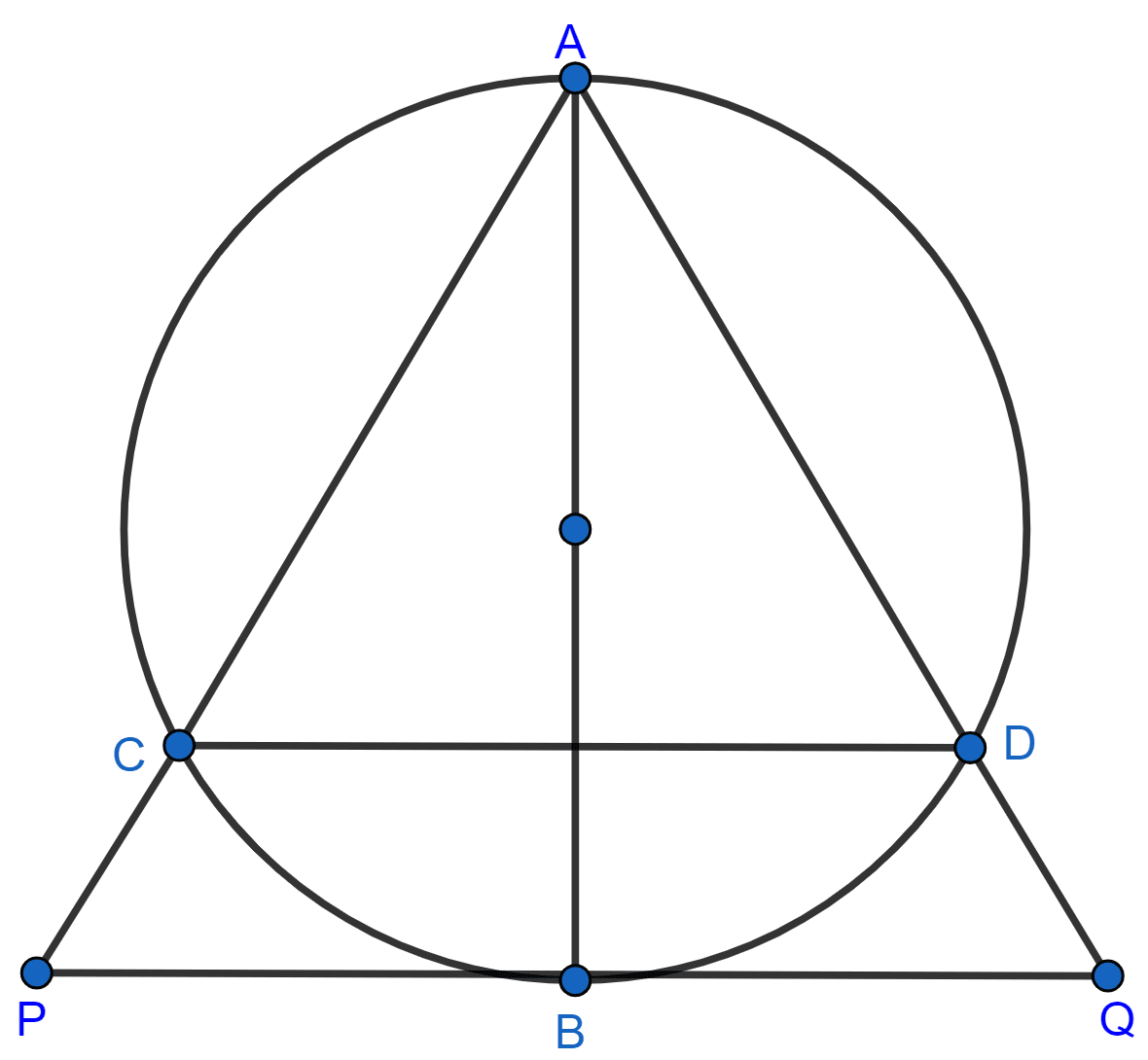
In the given figure, AB is a diameter of the circle. Chords AC and AD produced meet the tangent to the circle at point B in points P and Q respectively. Prove that :
AB2 = AC × AP
Use ruler and compasses for this question.
(i) Construct an isosceles triangle ABC in which AB = AC = 7.5 cm and BC = 6 cm.
(ii) Draw AD, the perpendicular from vertex A to side BC.
(iii) Draw a circle with center A and radius 2.8 cm, cutting AD at E.
(iv) Construct another circle to circumscribe the triangle BCE.
A conical vessel of radius 6 cm and height 8 cm is completely filled with water. A sphere is lowered into the water and its size is such that when it touches the sides it is just immersed . What fraction of water overflows ?
Prove that :
= 2(sec A + cosec A)