Mathematics
Two vertices of a triangle are (3, -5) and (-7, 4). Find the third vertex given that the centroid is (2, -1).
Section Formula
42 Likes
Answer
Let the coordinates of third vertex be (x, y) and other two vertices are (3, -5) and (-7, 4) and centroid = (2, -1).
Coordinates of Centroid of the triangle are given by
Hence, the coordinates of centroid are (10, -2).
Answered By
28 Likes
Related Questions
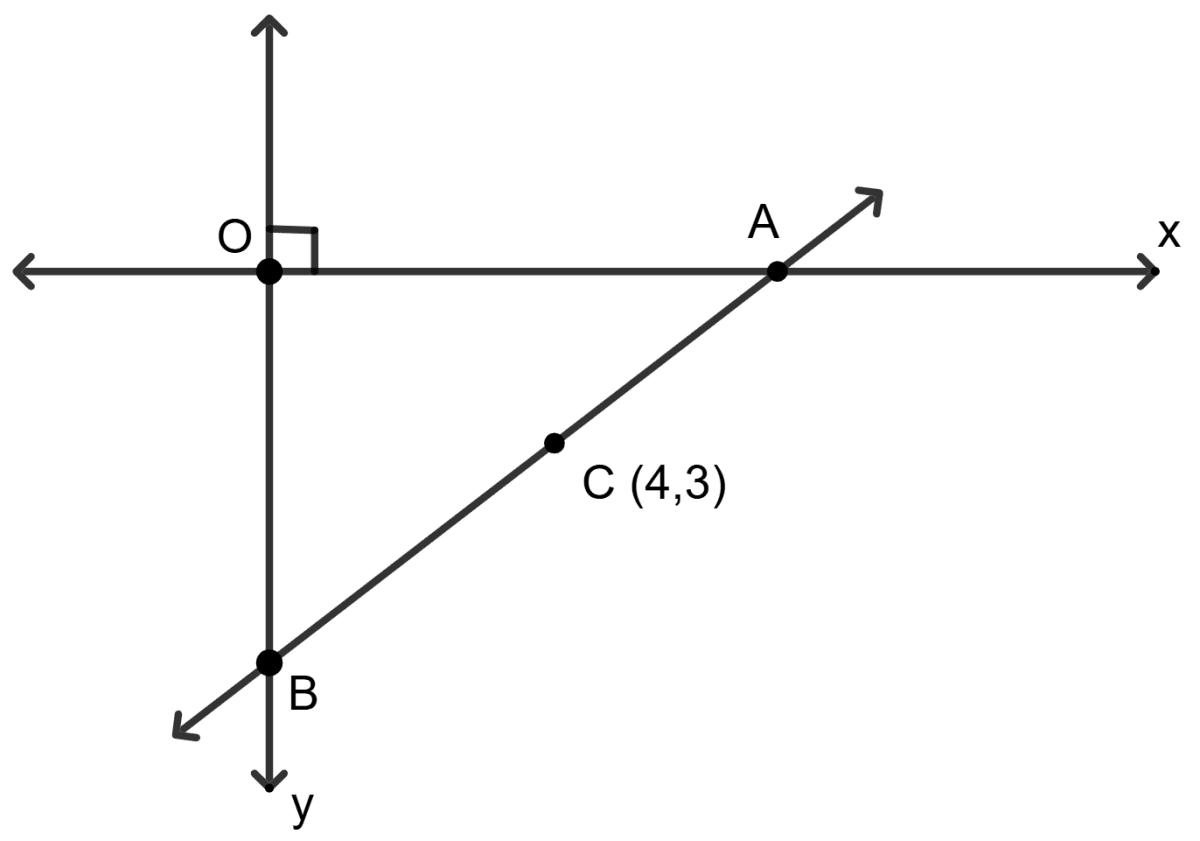
The mid-point of the line segment AB shown in diagram is C (4, -3). Write down the coordinates of A and B.
Find the coordinates of the centroid of a triangle whose vertices are :
A(-1, 3), B(1, -1) and C(5, 1).
The vertices of a triangle are A(-5, 3), B(p, -1) and C(6, q). Find the values of p and q if the centroid of the triangle ABC is the point (1, -1).
The points A(9, 0), B(9, 6), C(-9, 6) and D(-9, 0) are the vertices of a
rectangle
square
rhombus
trapezium