Mathematics
Two parallel tangents of a circle meet a third tangent at points P and Q. Prove that PQ subtends a right angle at the centre.
Circles
3 Likes
Answer
Let PA and QB be the two parallel tangents of the circle with centre O and PQ is the third tangent:
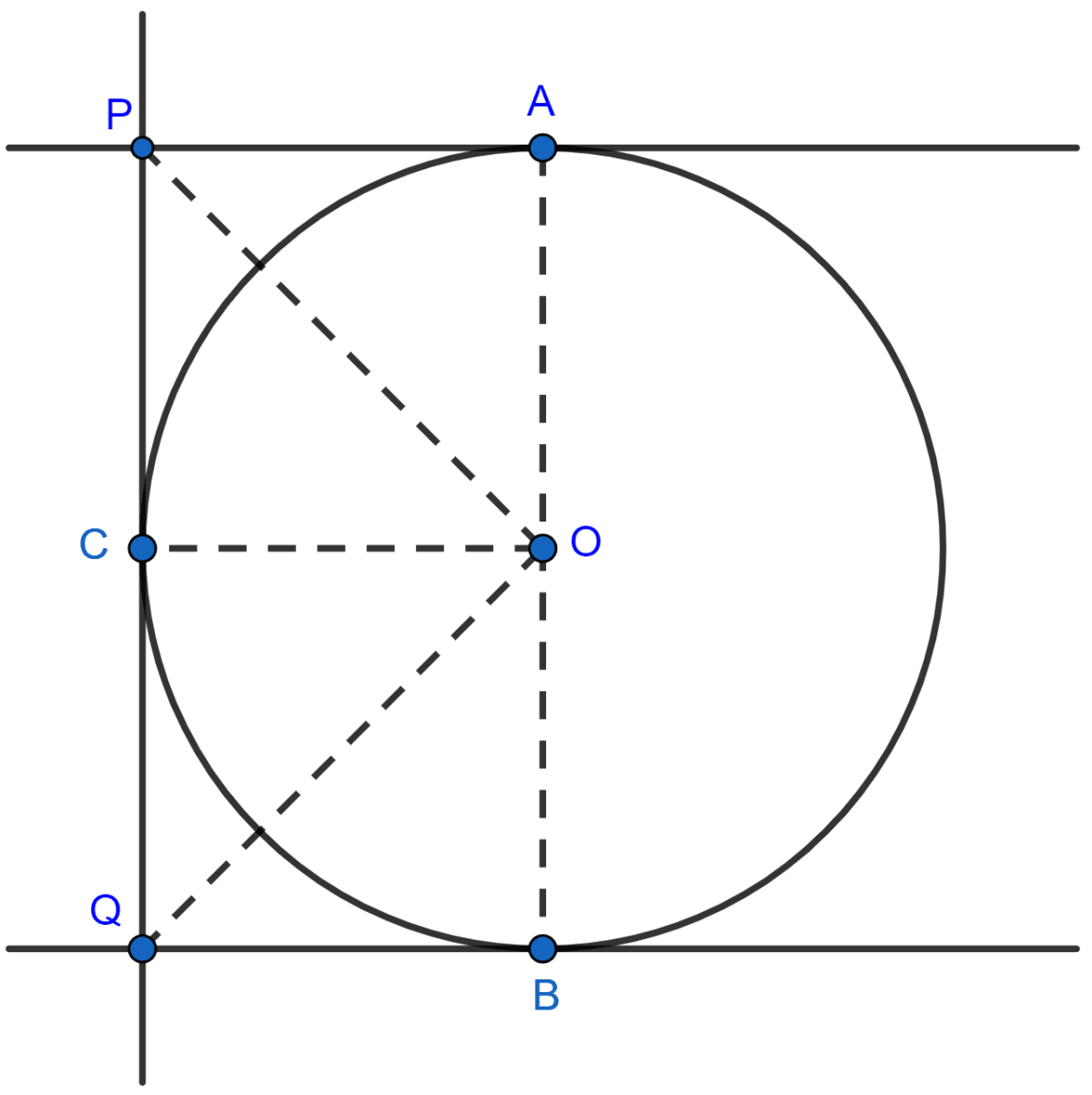
In △OAP and △OCP,
⇒ OA = OC [Radius of same circle]
⇒ OP = OP [Common]
⇒ PA = PC [∵ Tangents from exterior point P are equal in length.]
∴ △OAP ≅ △OCP [By SSS axiom]
∴ ∠APO = ∠CPO [By C.P.C.T.]
⇒ ∠APC = ∠APO + ∠CPO
⇒ ∠APC = 2∠CPO ………..(1)
In △OBQ and △OCQ,
⇒ OB = OC [Radius of same circle]
⇒ OQ = OQ [Common]
⇒ QB = QC [∵ Tangents from exterior point P are equal in length.]
∴ △OBQ ≅ △OCQ [By SSS axiom]
∴ ∠CQO = ∠BQO [By C.P.C.T.]
⇒ ∠CQB = ∠CQO + ∠BQO
⇒ ∠CQB = 2∠CQO ………..(2)
As, sum of co-interior angles between parallel lines = 180°.
⇒ ∠APC + ∠CQB = 180°
⇒ 2∠CPO + 2∠CQO = 180° [From (1) and (2)]
⇒ ∠CPO + ∠CQO = 90° ……….(3)
In △POQ,
⇒ ∠CPO + ∠CQO + ∠POQ = 180° [Angle sum property of triangle]
⇒ 90° + ∠POQ = 180°
⇒ ∠POQ = 180° - 90°
⇒ ∠POQ = 90°.
Hence, proved that PQ subtends a right angle at the centre.
Answered By
1 Like
Related Questions
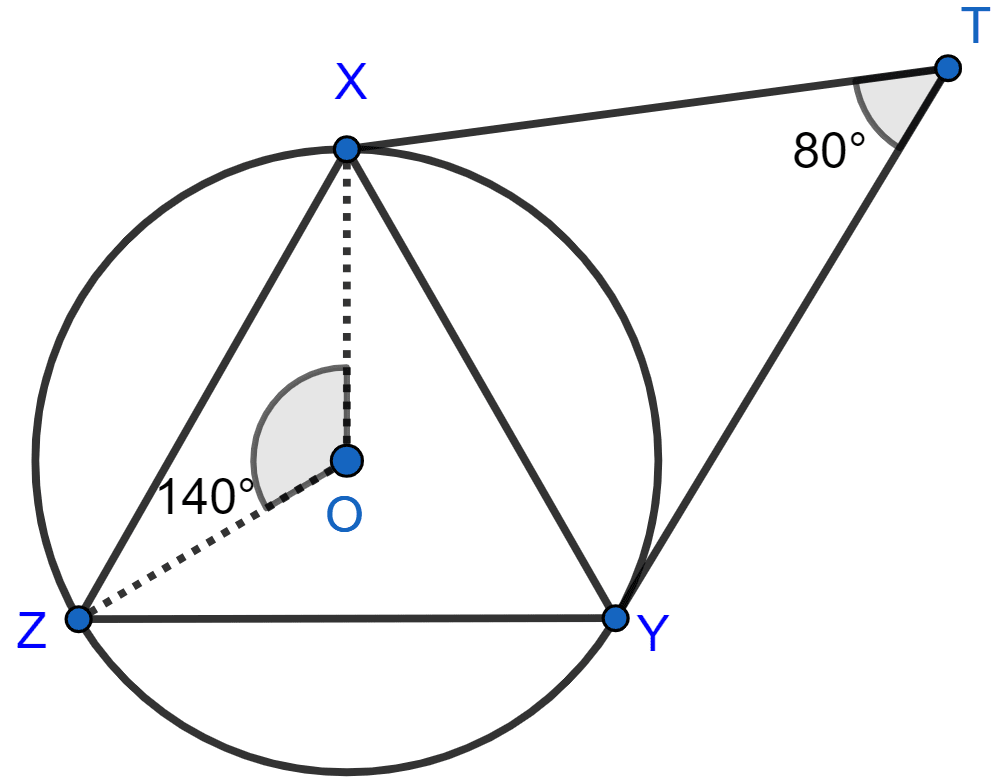
In the figure, given below, O is the center of the circumcircle of triangle XYZ. Tangents at X and Y intersect at point T. Given ∠XTY = 80° and ∠XOZ = 140°, calculate the value of ∠ZXY.
In the given figure, AE and BC intersect each other at point D. If ∠CDE = 90°, AB = 5 cm, BD = 4 cm and CD = 9 cm, find AE.

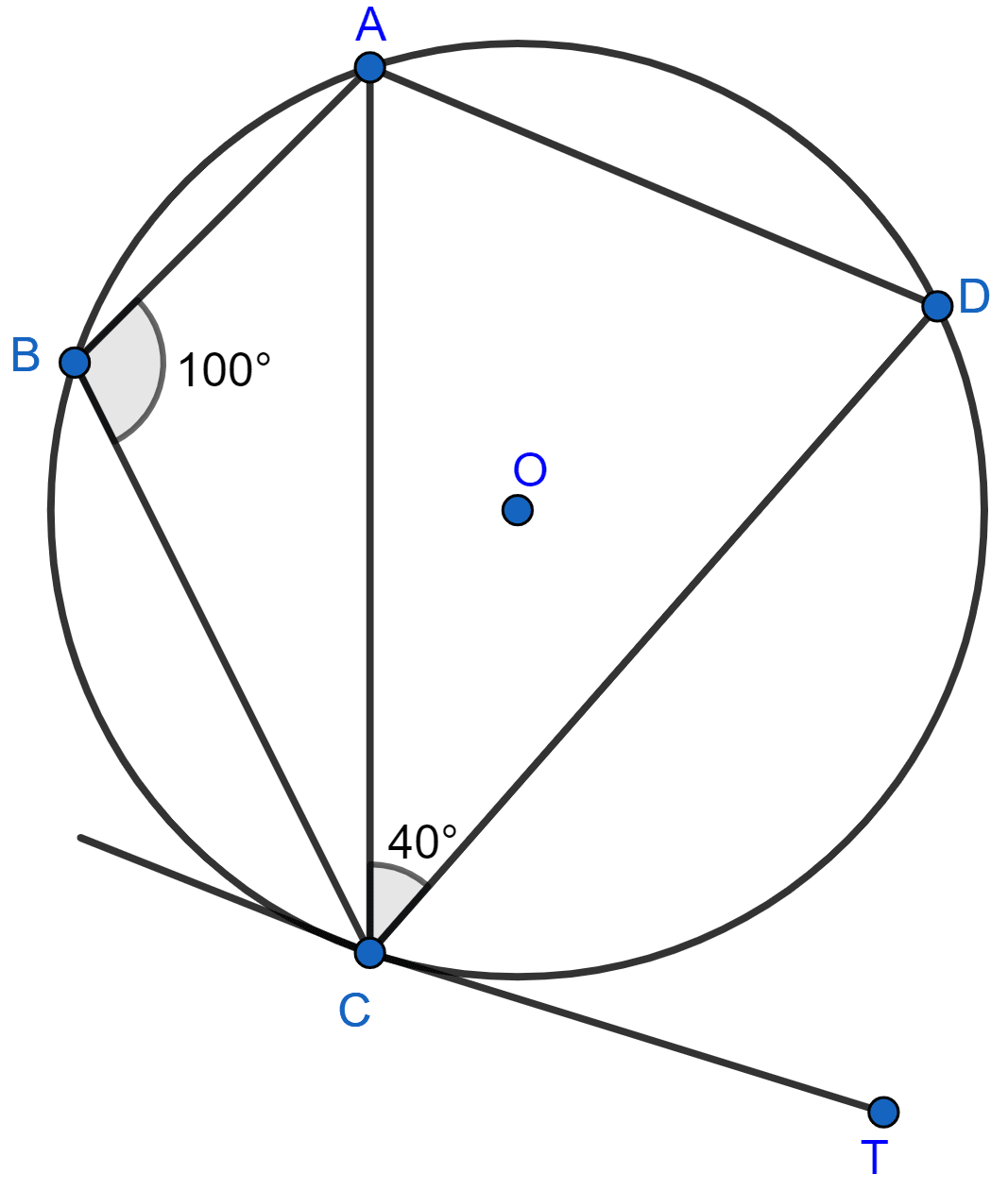
In the given circle with centre O, angle ABC = 100°, ∠ACD = 40° and CT is a tangent to the circle at C. Find ∠ADC and ∠DCT.
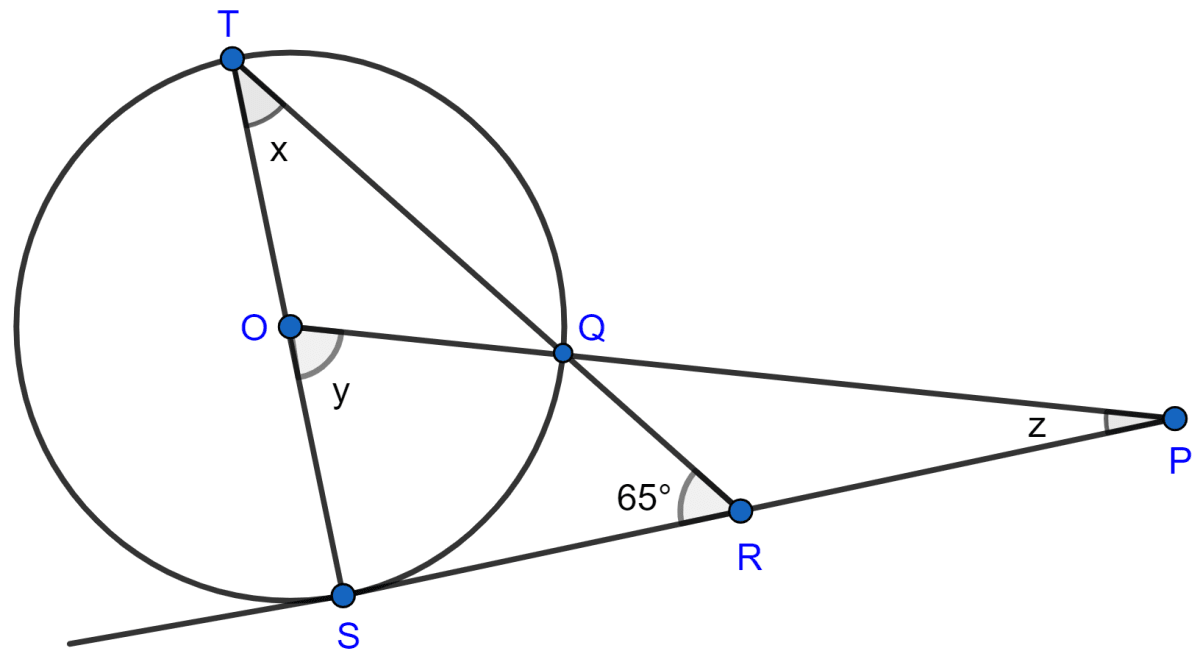
In the figure given below, O is the center of the circle and SP is a tangent. If ∠SRT = 65°, find the values of x, y and z.