Mathematics
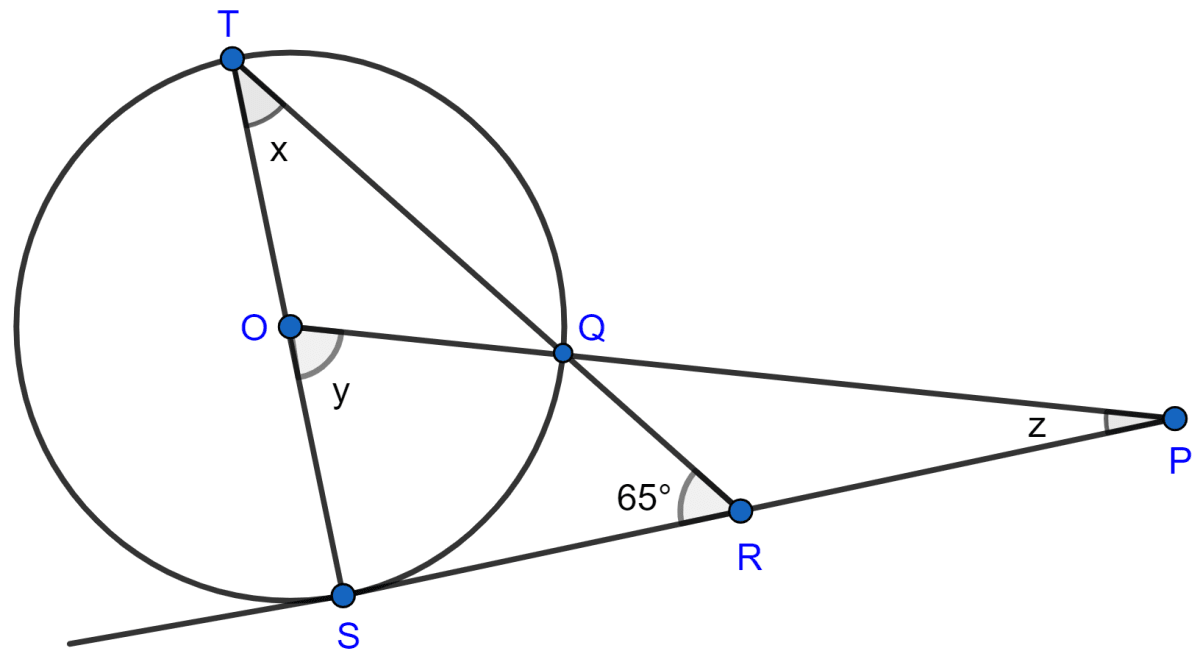
In the figure given below, O is the center of the circle and SP is a tangent. If ∠SRT = 65°, find the values of x, y and z.
Circles
1 Like
Answer
As, SP is tangent to the circle.
∴ ∠TSR = 90°.
In △TSR,
⇒ ∠TSR + ∠STR + ∠SRT = 180° [By angle sum property of triangle]
⇒ 90° + x + 65° = 180°
⇒ x = 180° - 155° = 25°.
We know that,
Angle which an arc subtends at the center is double that which it subtends at any point on the remaining part of the circumference.
∴ ∠SOQ = 2∠STQ
⇒ y = 2x = 2(25°) = 50°.
In △OSP,
⇒ ∠OSP + ∠SOP + ∠SPO = 180° [By angle sum property of triangle]
⇒ 90° + y + z = 180°
⇒ 90° + 50° + z = 180°
⇒ z = 180° - 140° = 40°.
Hence, x = 25°, y = 50° and z = 40°.
Answered By
1 Like
Related Questions
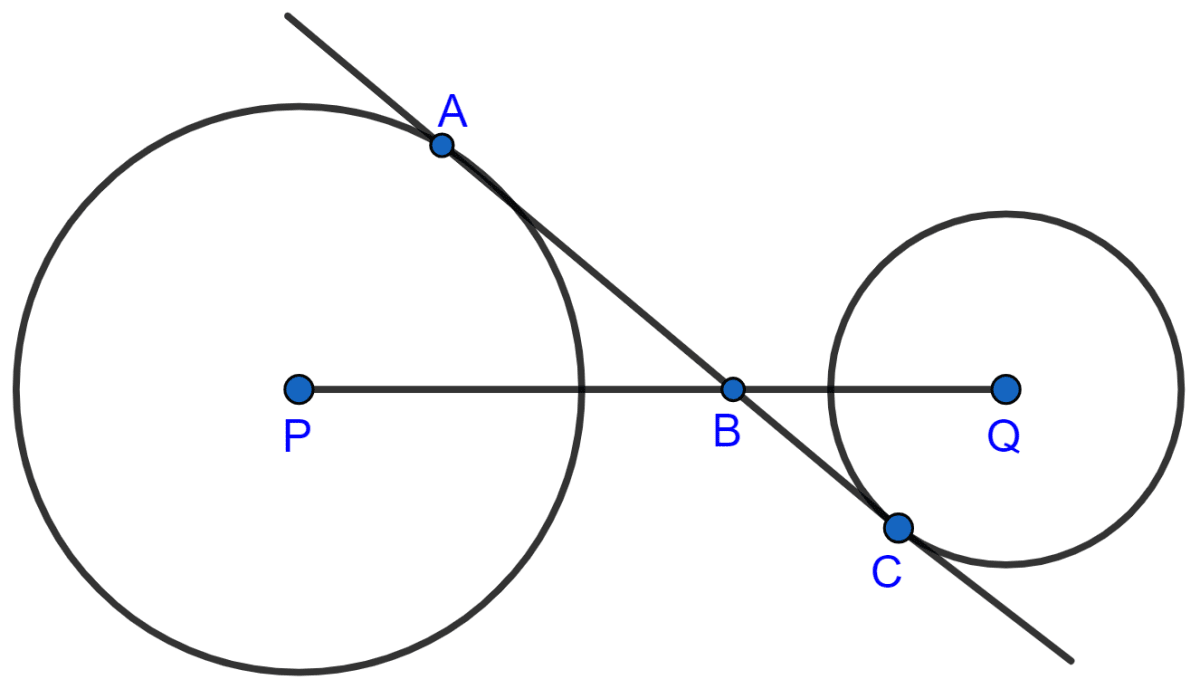
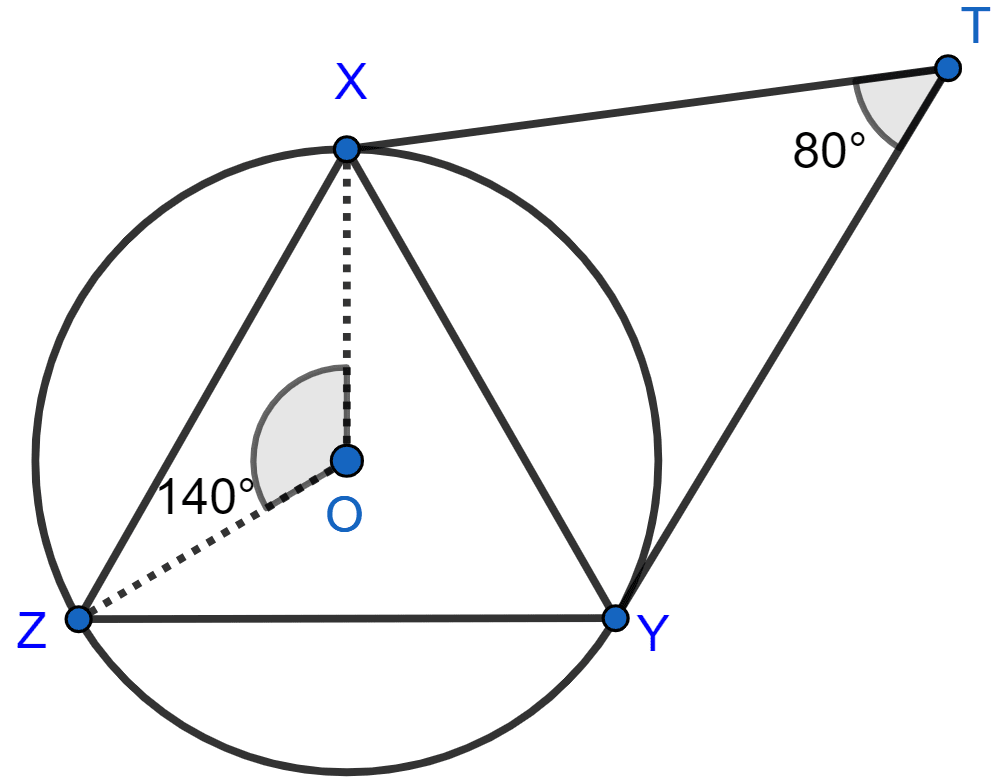
In the figure, given below, O is the center of the circumcircle of triangle XYZ. Tangents at X and Y intersect at point T. Given ∠XTY = 80° and ∠XOZ = 140°, calculate the value of ∠ZXY.
In the given figure, AE and BC intersect each other at point D. If ∠CDE = 90°, AB = 5 cm, BD = 4 cm and CD = 9 cm, find AE.
In the figure, given below, AC is a transverse common tangent to two circles with centers P and Q and of radii 6 cm and 3 cm respectively. Given that AB = 8 cm, calculate PQ.
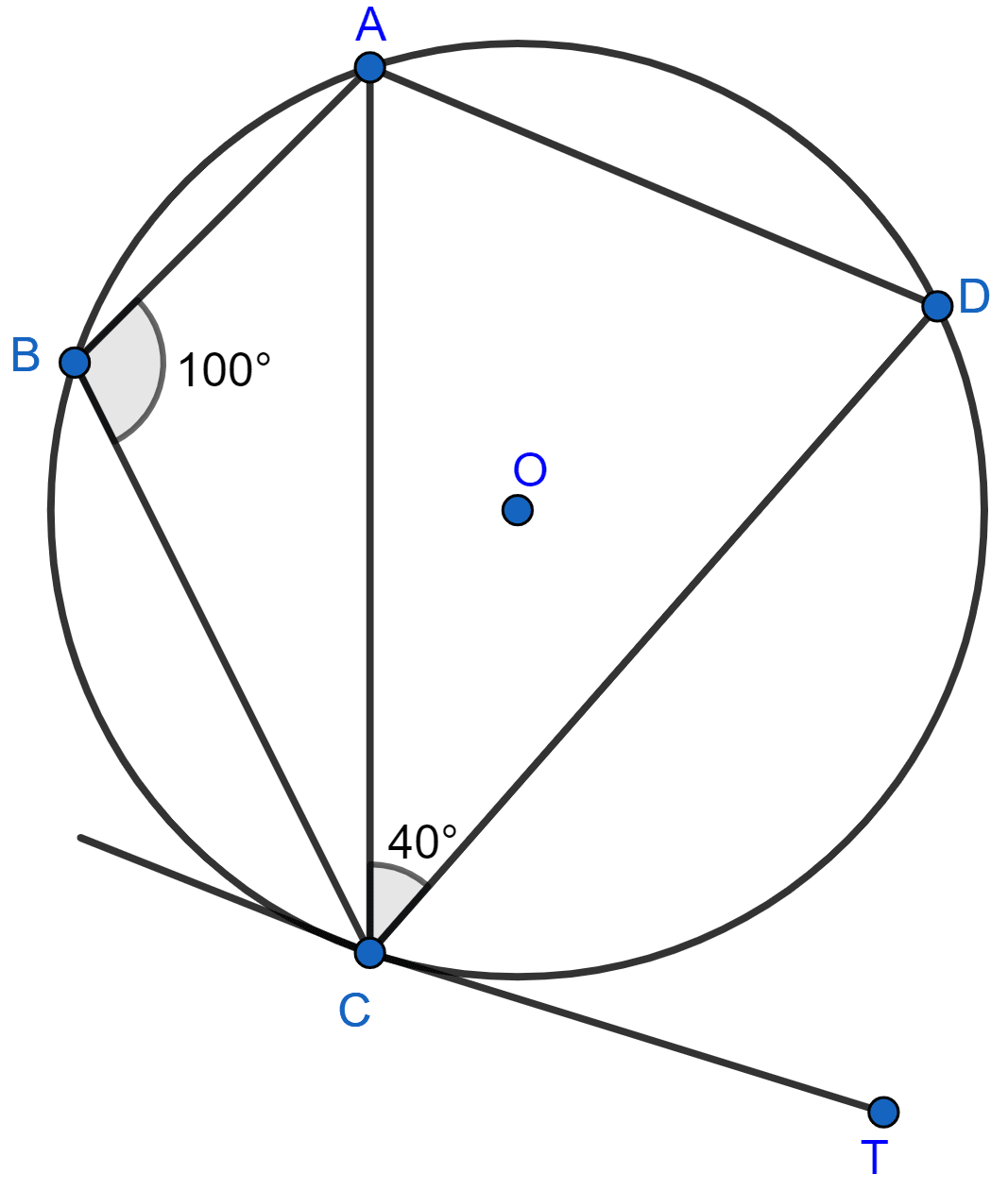
In the given circle with centre O, angle ABC = 100°, ∠ACD = 40° and CT is a tangent to the circle at C. Find ∠ADC and ∠DCT.
