Mathematics
Two circles with centres A, B are of radii 6 cm and 3 cm respectively. If AB = 15 cm, find the length of a transverse common tangent to these circles.
Circles
Answer
The two circles with centres A, B are of radii 6 cm and 3 cm and AB = 15 cm are shown in the figure below:
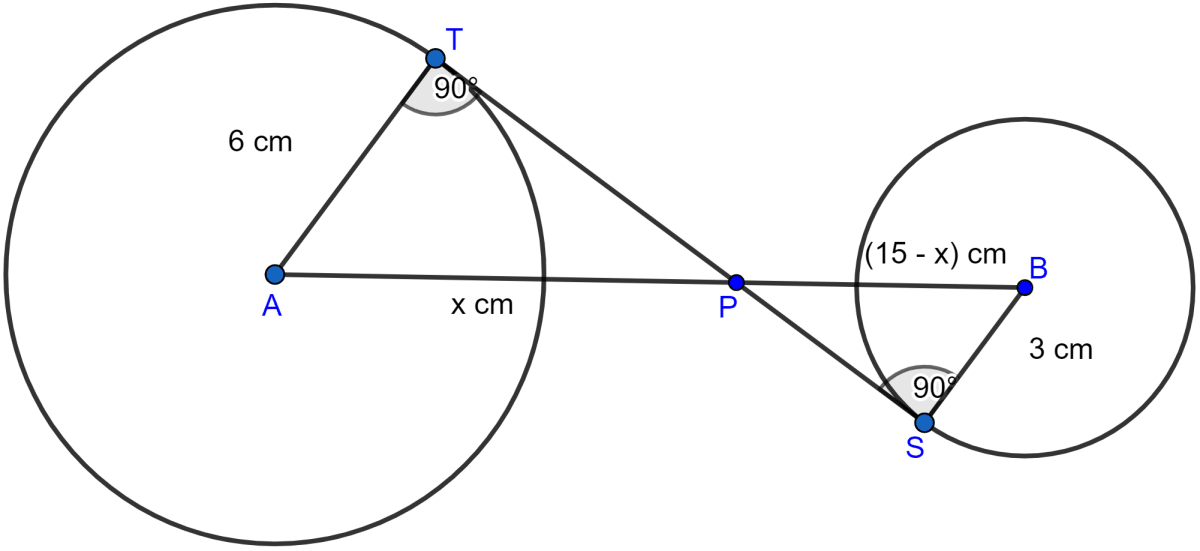
Given, AB = 15 cm.
Let AP = x, then PB = 15 - x
Considering △ATP and △SBP,
∠T = ∠S (Each are equal to 90°)
∠APT = ∠BPS (Vertically opposite angles are equal)
△ATP ~ △SBP by AA axiom.
Since triangles are similar hence, the ratio of their corresponding sides are equal.
∴ AP = 10 cm,
From figure,
PB = AB - AP = 15 - 10 = 5 cm.
Now in right-angled triangle ATP,
Similarly in right angled triangle PSB,
Hence, TS = TP + PS = 8 + 4 = 12 cm.
Hence, the length of a transverse common tangent to these circles are 12 cm.
Answered By
Related Questions
Calculate the length of a direct common tangent to two circles of radii 3 cm and 8 cm with their centres 13 cm apart.
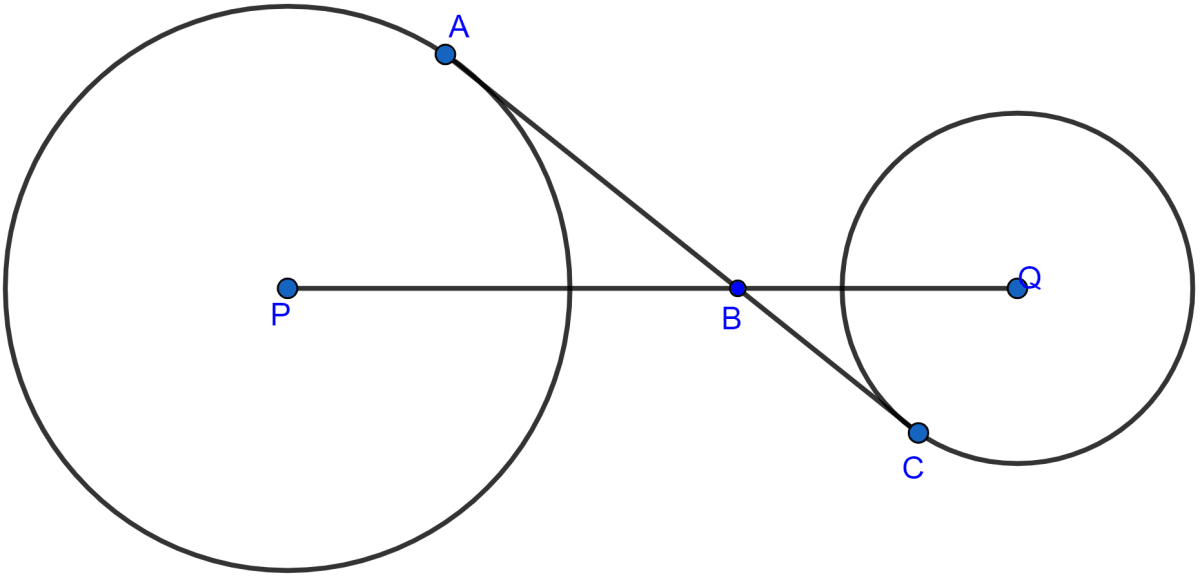
In the given figure, AC is a transverse common tangent to two circles with centres P and Q and of radii 6 cm and 3 cm respectively. Given that AB = 8 cm, calculate PQ.
In the figure (i) given below, PA and PB are tangents at the points A and B respectively of a circle with centre O. Q and R are points on the circle If ∠APB = 70°, find
(i) ∠AOB
(ii) ∠AQB
(iii) ∠ARB

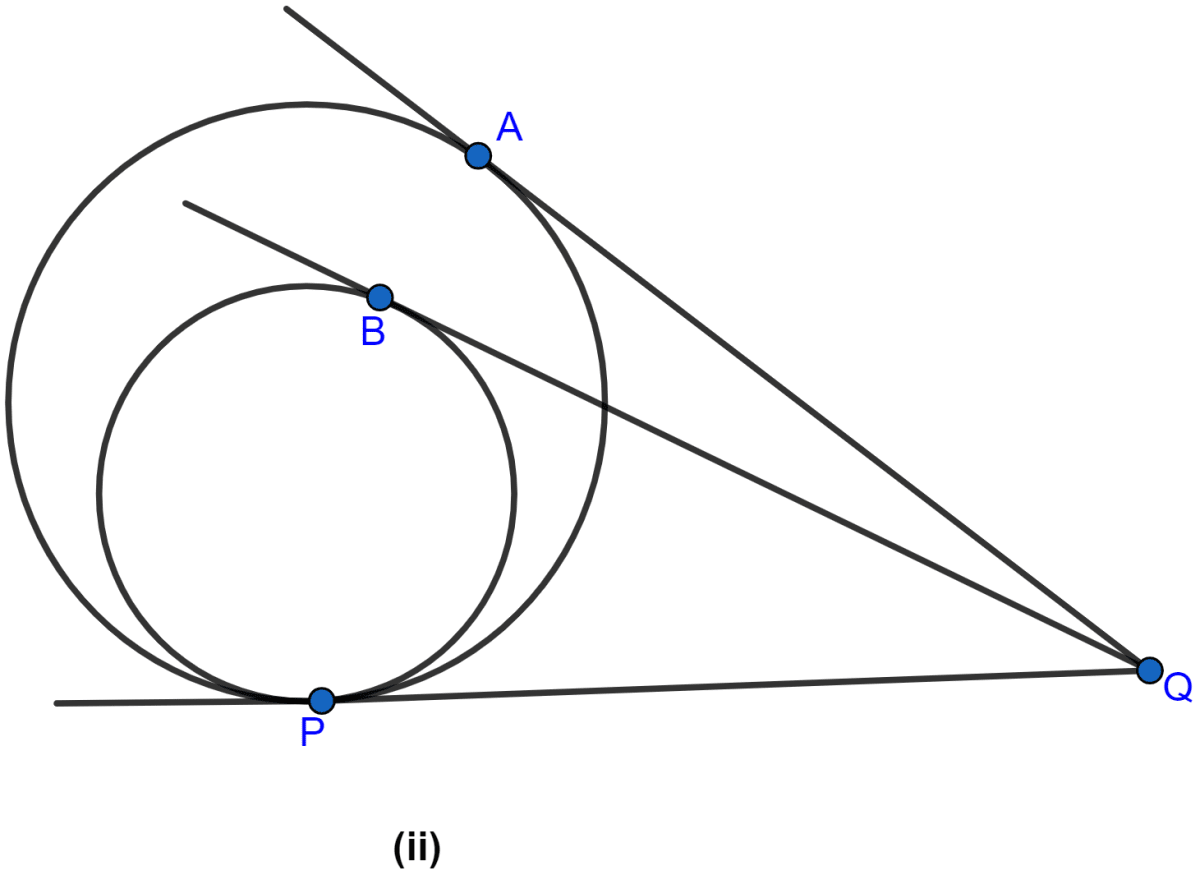
In the figure (ii) given below, two circles touch internally at P from an external point Q on the common tangent at P, two tangents QA and QB are drawn to the two circles. Prove that QA = QB.