Mathematics
Two circles touch each other internally at a point P. A chord AB of the bigger circle intersects the other circle in C and D. Prove that : ∠CPA = ∠DPB.
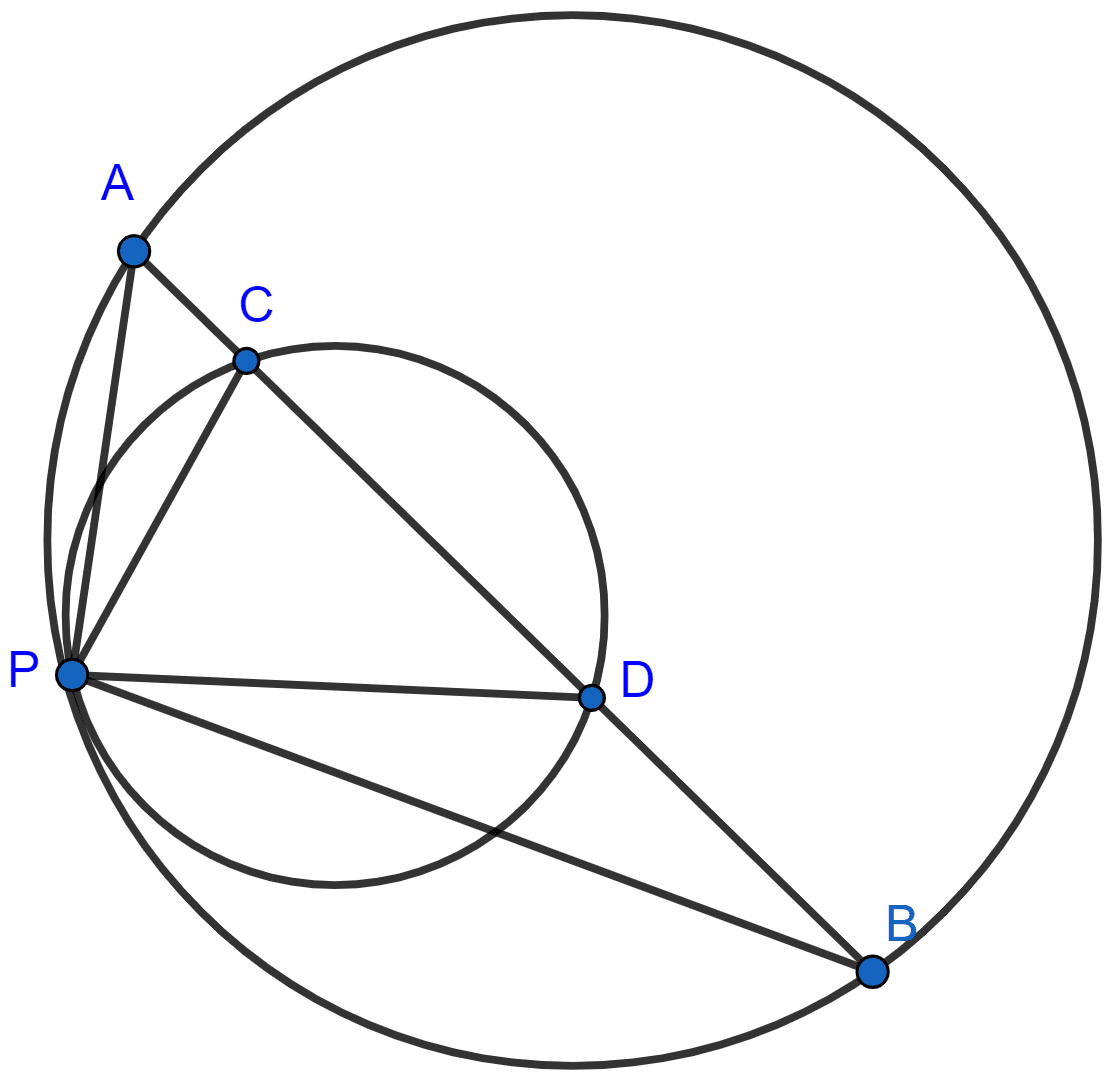
Answer
Draw tangent at point P,
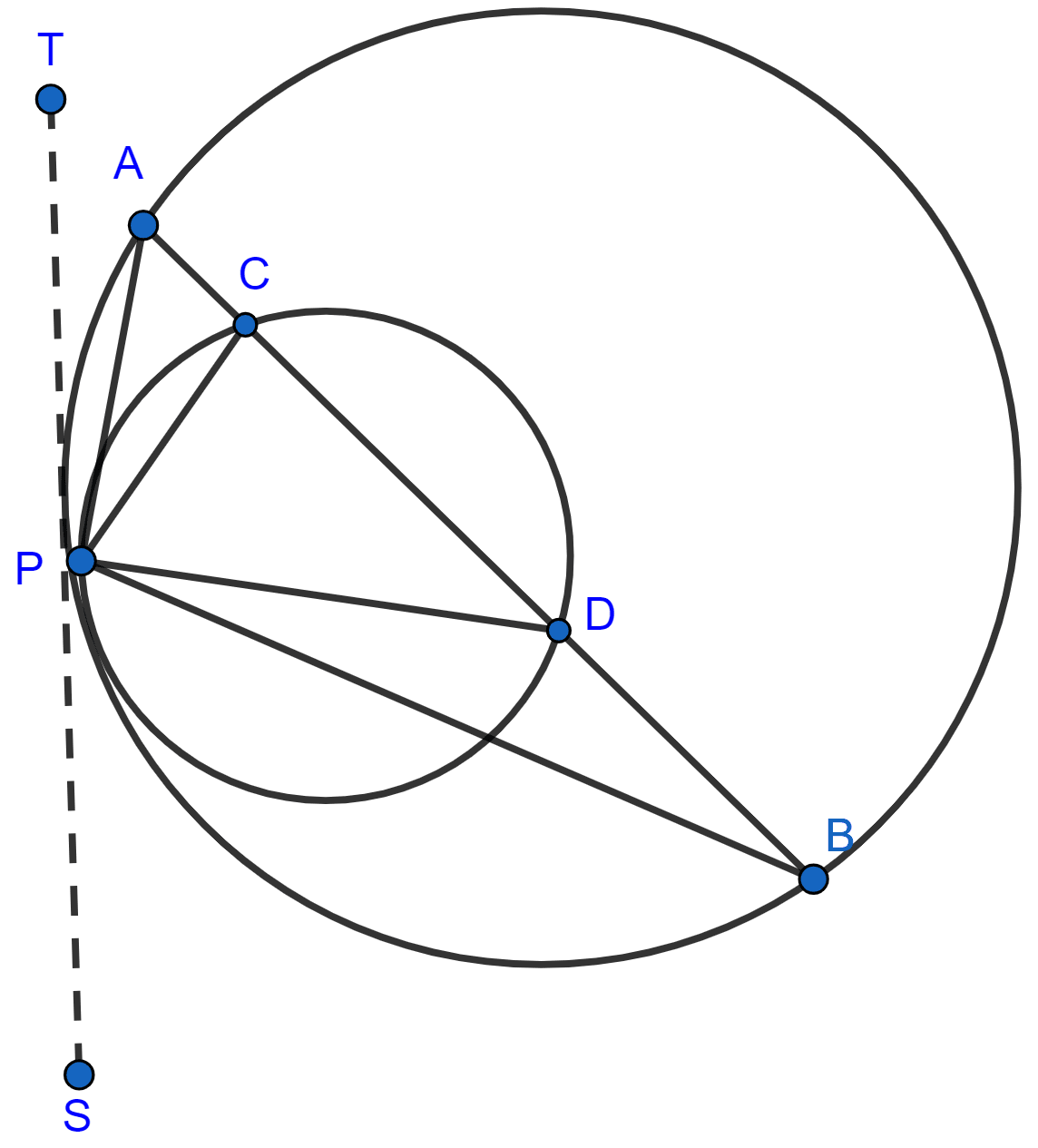
∠PAB = ∠BPS ………….(1) [Angles in alternate segments are equal.]
∠PCD = ∠DPS ………….(2) [Angles in alternate segments are equal.]
Subtracting (1) from (2), we get :
⇒ ∠PCD - ∠PAB = ∠DPS - ∠BPS …………(3)
In △PAC,
⇒ ∠PCD = ∠PAC + ∠CPA [An exterior angle is equal to sum of two opposite interior angles.]
⇒ ∠PCD = ∠PAB + ∠CPA [From figure, ∠PAC = ∠PAB]
Substituting above value of ∠PCD in (3), we get :
⇒ ∠PAB + ∠CPA - ∠PAB = ∠DPS - ∠BPS
⇒ ∠CPA = ∠DPB [From figure, ∠DPS - ∠BPS = ∠DPB].
Hence, proved that ∠CPA = ∠DPB.
Related Questions
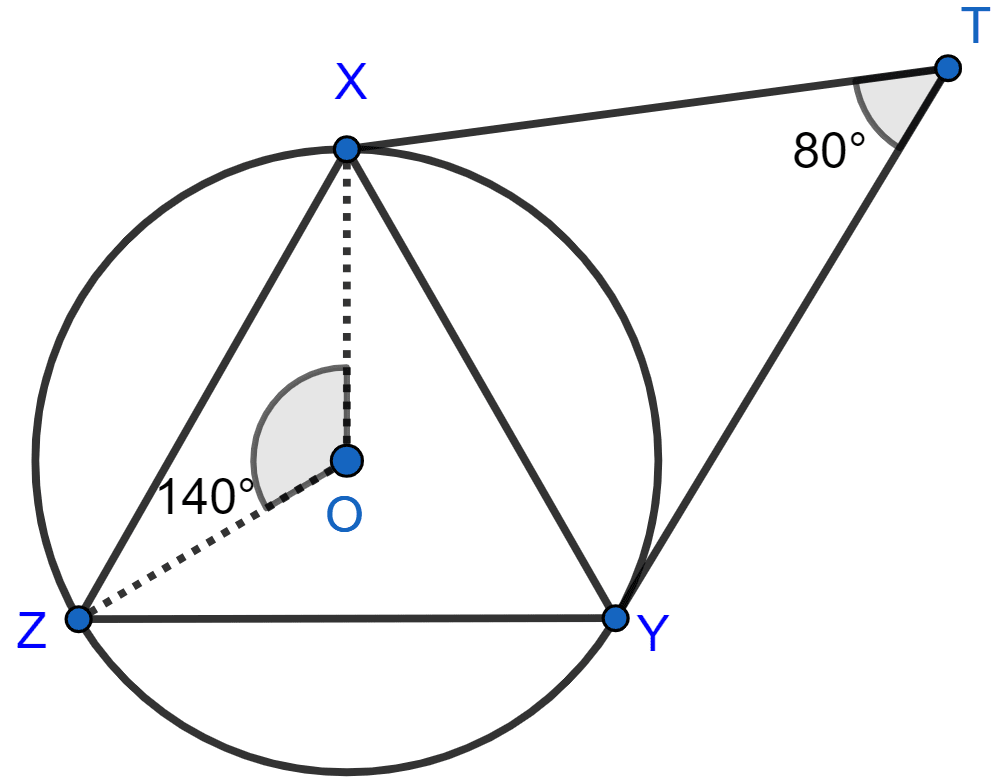
In the figure, given below, O is the center of the circumcircle of triangle XYZ. Tangents at X and Y intersect at point T. Given ∠XTY = 80° and ∠XOZ = 140°, calculate the value of ∠ZXY.
In the given figure, AE and BC intersect each other at point D. If ∠CDE = 90°, AB = 5 cm, BD = 4 cm and CD = 9 cm, find AE.

In the given circle with centre O, angle ABC = 100°, ∠ACD = 40° and CT is a tangent to the circle at C. Find ∠ADC and ∠DCT.
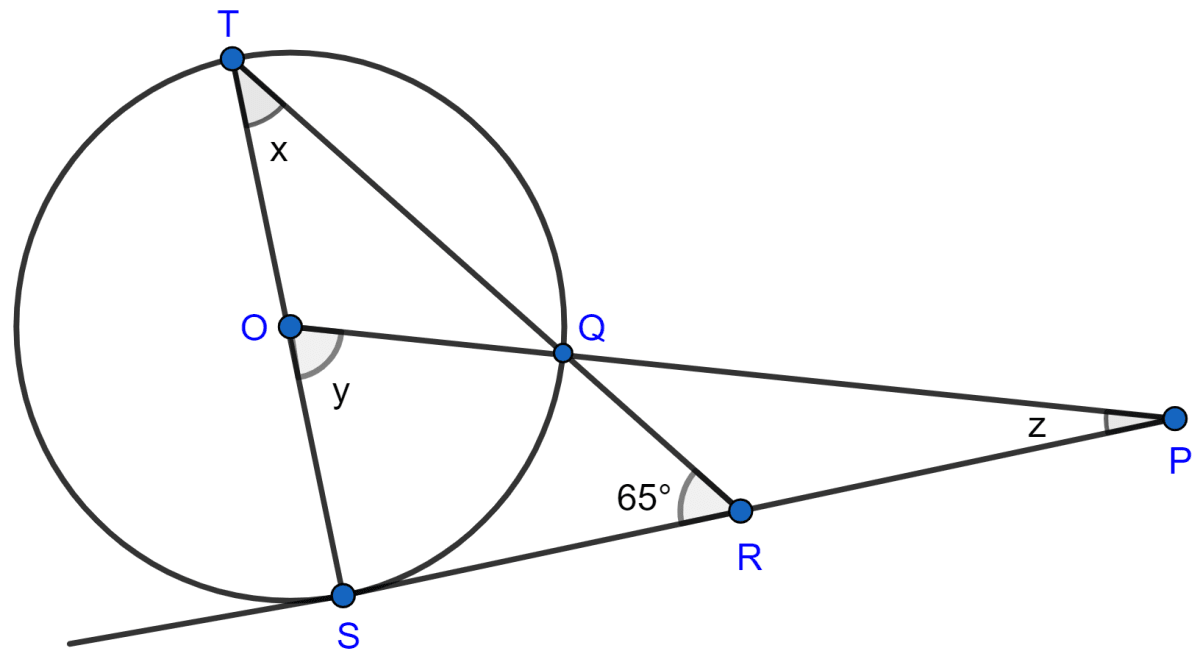
In the figure given below, O is the center of the circle and SP is a tangent. If ∠SRT = 65°, find the values of x, y and z.