Mathematics
Two chords AB, CD of a circle intersect externally at a point P. If PB = 7 cm, AB = 9 cm and PD = 6 cm, find CD.
Circles
5 Likes
Answer
We know that,
If two chords of a circle intersect externally, then the products of the length of segments are equal.
From figure,
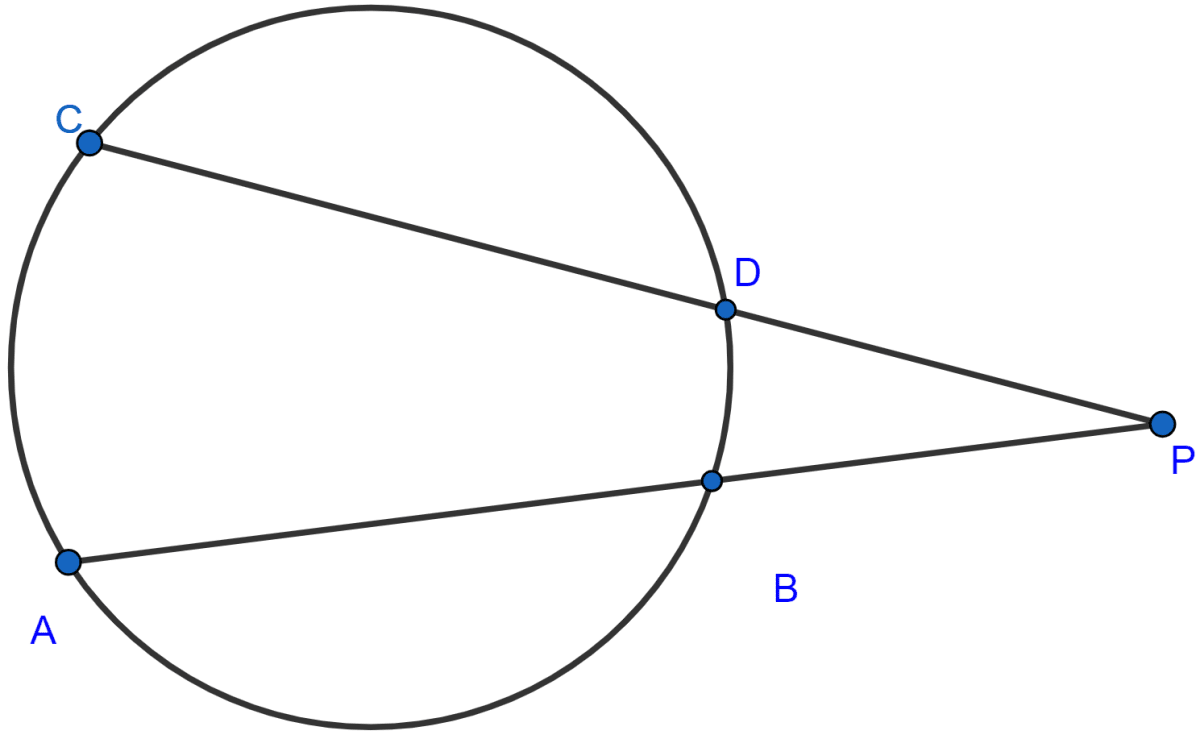
PA.PB = PC.PD …..(i)
PA = PB + AB = 7 + 9 = 16 cm.
Putting values in equation (i) we get,
⇒ 16 × 7 = PC × 6
⇒ 112 = PC × 6
⇒ PC =
⇒ PC = .
From figure,
CD = PC - PD =
Hence, the value of CD = cm.
Answered By
3 Likes
Related Questions
In the figure (ii) given below, chord AB and diameter CD of a circle meet at P. If AB = 8 cm, BP = 6 cm and PD = 4 cm, find the radius of the circle. Also find the length of the tangent drawn from P to the circle.

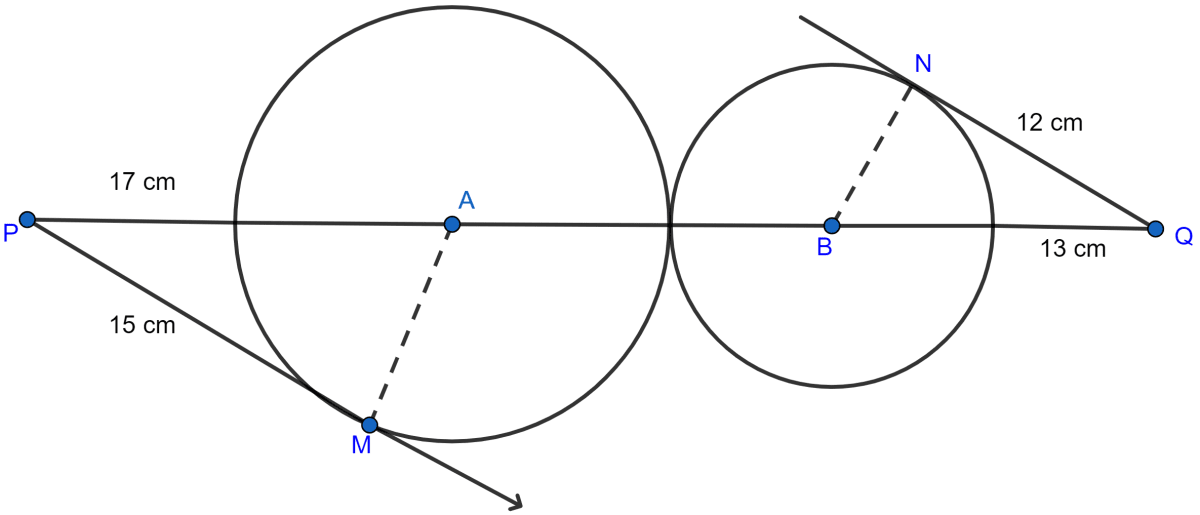
In the figure given below, two circles with centres A and B touch externally. PM is a tangent to the circle with centre A and QN is a tangent to the circle with centre B. If PM = 15 cm, QN = 12 cm, PA = 17 cm and QB = 13 cm, then find the distance between the centres A and B of the circles.
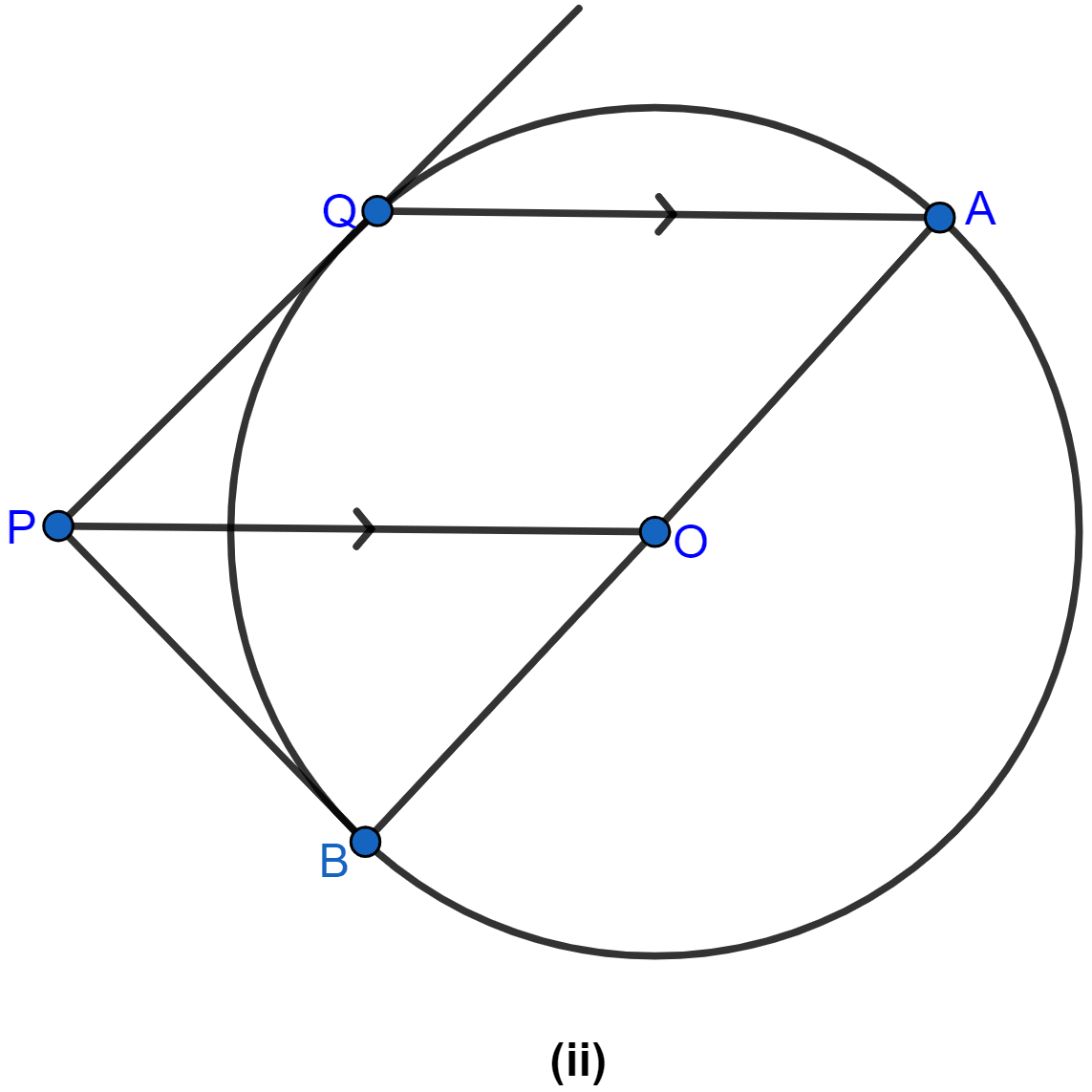
In the figure (ii) given below, PQ is a tangent to the circle with centre O and AB is a diameter of the circle. If QA is parallel to PO, prove that PB is tangent to the circle.
In the figure (i) given below, chord AB and diameter CD of a circle with centre O meet at P. PT is tangent to the circle at T. If AP = 16 cm, AB = 12 cm and DP = 2 cm, find the length of PT and the radius of the circle.
