Mathematics
Two chords AB and AC of a circle are equal. Prove that the center of the circle, lies on the bisector of the angle BAC.
Answer
Given,
AB and AC are two equal chords of circle with center O and radius r.
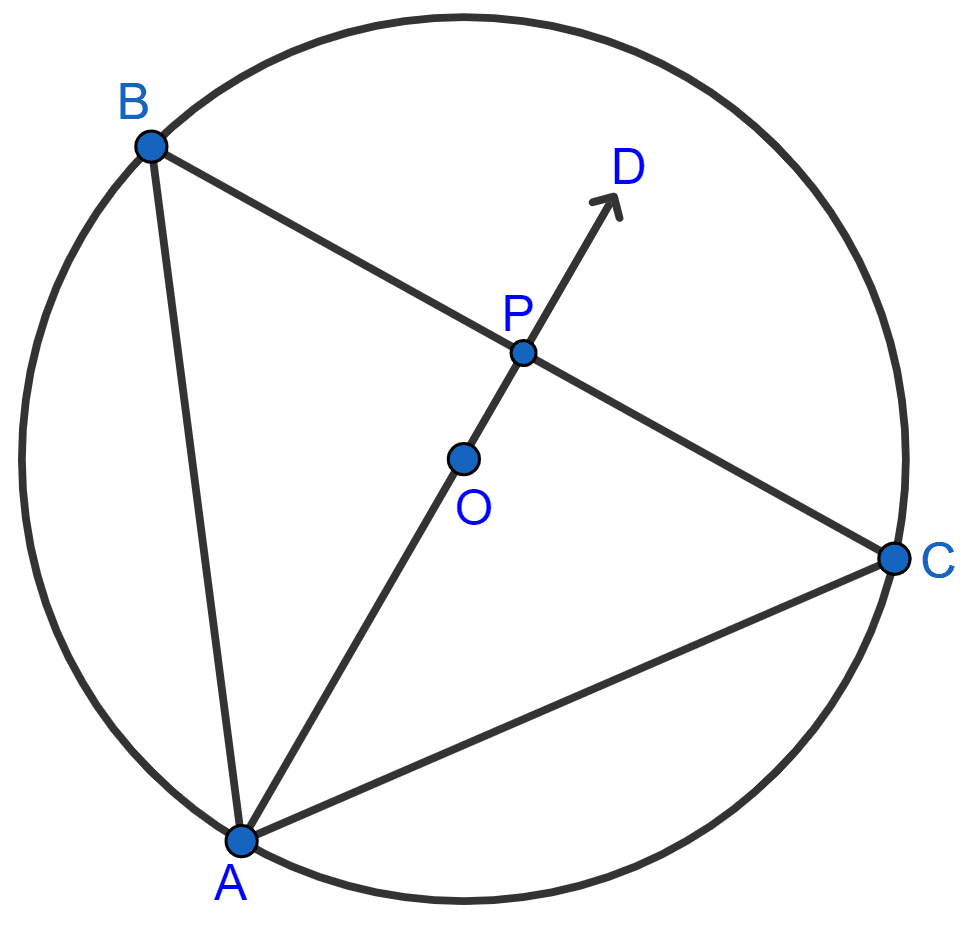
In ∆APB and ∆APC,
⇒ AB = AC [Given]
⇒ ∠BAP = ∠CAP [Given]
⇒ AP = AP [Common]
Hence, ∆APB ≅ ∆APC by SAS axiom.
By CPCT, we get :
BP = CP and ∠APB = ∠APC
From figure,
⇒ ∠APB + ∠APC = 180° [Linear pairs]
⇒ 2∠APB = 180°
⇒ ∠APB = 90°
Since, BP = CP and ∠APB = 90°.
∴ AP is the perpendicular bisector of chord BC.
∵ The perpendicular bisector of a chord passes through the centre of the circle.
∴ AD is the bisector of ∠BAC and passes through the centre O of the circle.
Hence proved that, AD passes through the centre of the circle.
Related Questions
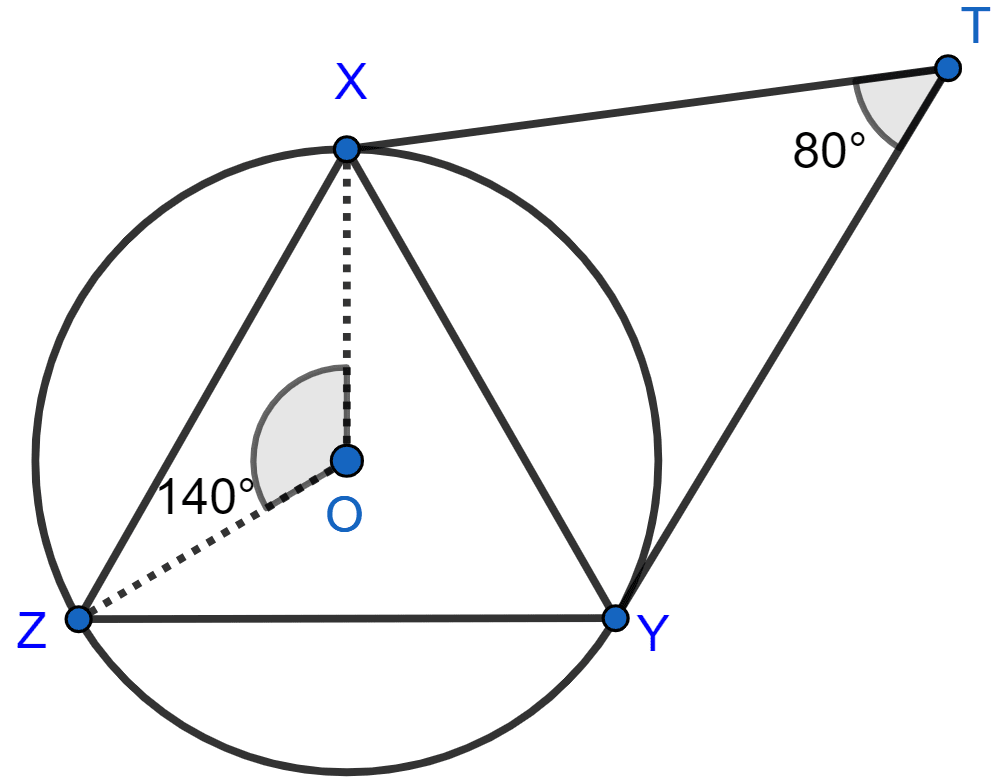
In the figure, given below, O is the center of the circumcircle of triangle XYZ. Tangents at X and Y intersect at point T. Given ∠XTY = 80° and ∠XOZ = 140°, calculate the value of ∠ZXY.
In the given figure, AE and BC intersect each other at point D. If ∠CDE = 90°, AB = 5 cm, BD = 4 cm and CD = 9 cm, find AE.

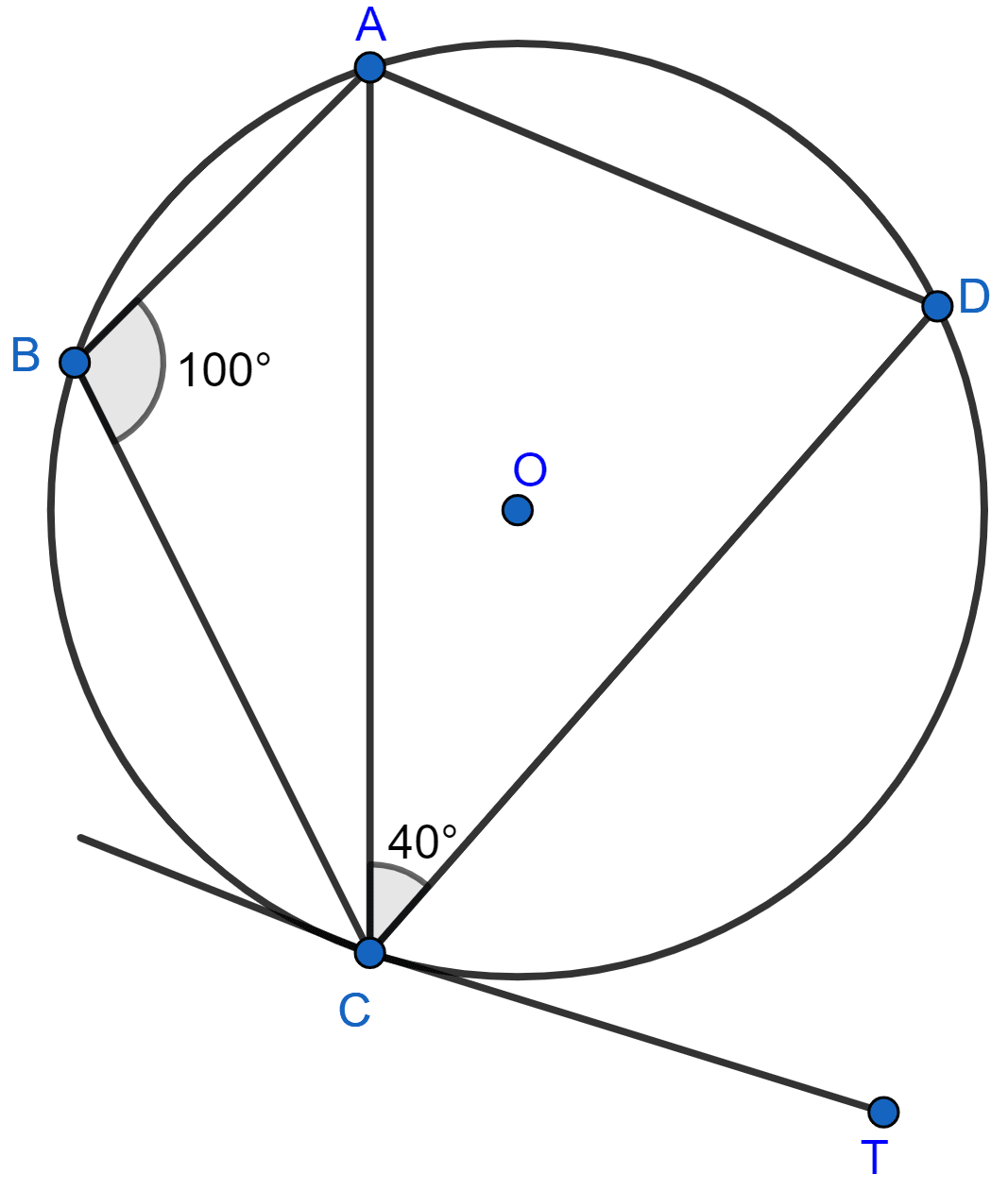
In the given circle with centre O, angle ABC = 100°, ∠ACD = 40° and CT is a tangent to the circle at C. Find ∠ADC and ∠DCT.
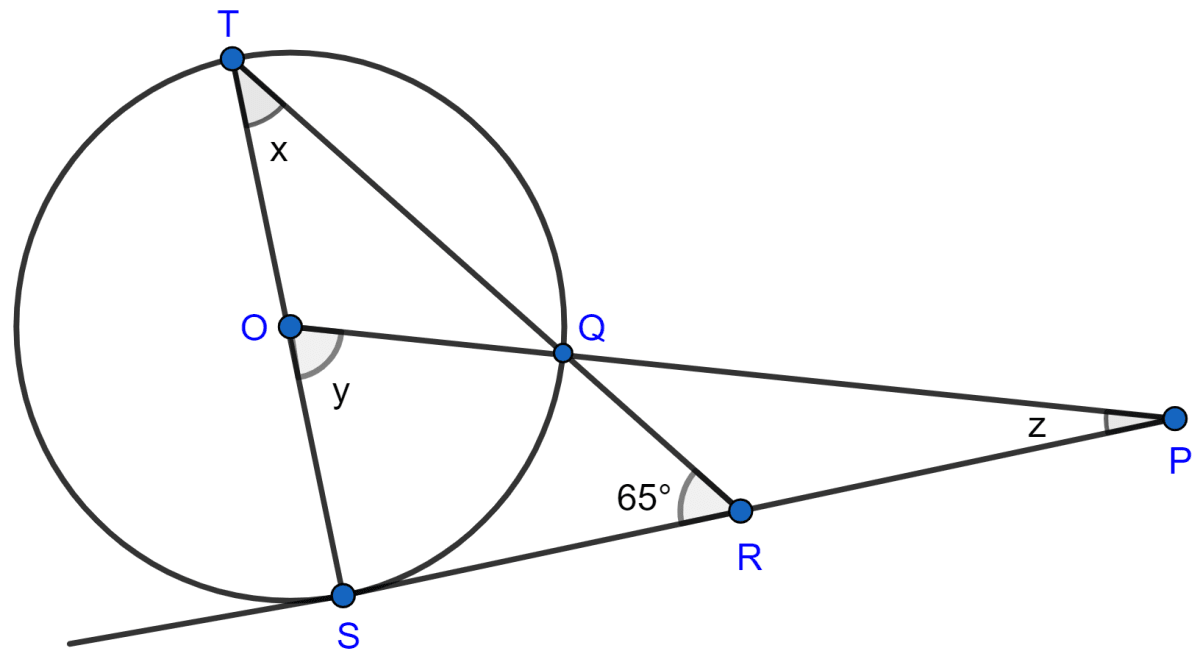
In the figure given below, O is the center of the circle and SP is a tangent. If ∠SRT = 65°, find the values of x, y and z.