Mathematics
Triangles ABC and PQR are similar to each other, then : 1. Ar.(△ABC)/Ar.(△PQR) = BC^2/PQ^2 2. AB^2/PQ^2 = AC^2/PR^2 3. Ar.(△BAC)/Ar.(△QPR) ≠ AB^2/QP^2 4. AC^2/PR^2 = BC^2/PQ^2
Related Questions
Triangles ABC and RSP are similar to each other, the corresponding sides of the two triangles are :
AB and RS
BC and RP
AC and SP
AB and RP
In △ABD, C is a point on side BD such that ∠ACD = ∠BAD. Is △BAD similar to triangle ACD? If yes, then which axiom is satisfied :
Yes, ASA
Yes, SAS
Yes, AA
No
A : Two similar triangles are congruent.
B : Two congruent triangles are similar, then :
A is true, B is false
A is false, B is true
A is false, B is false
A is true, B is true
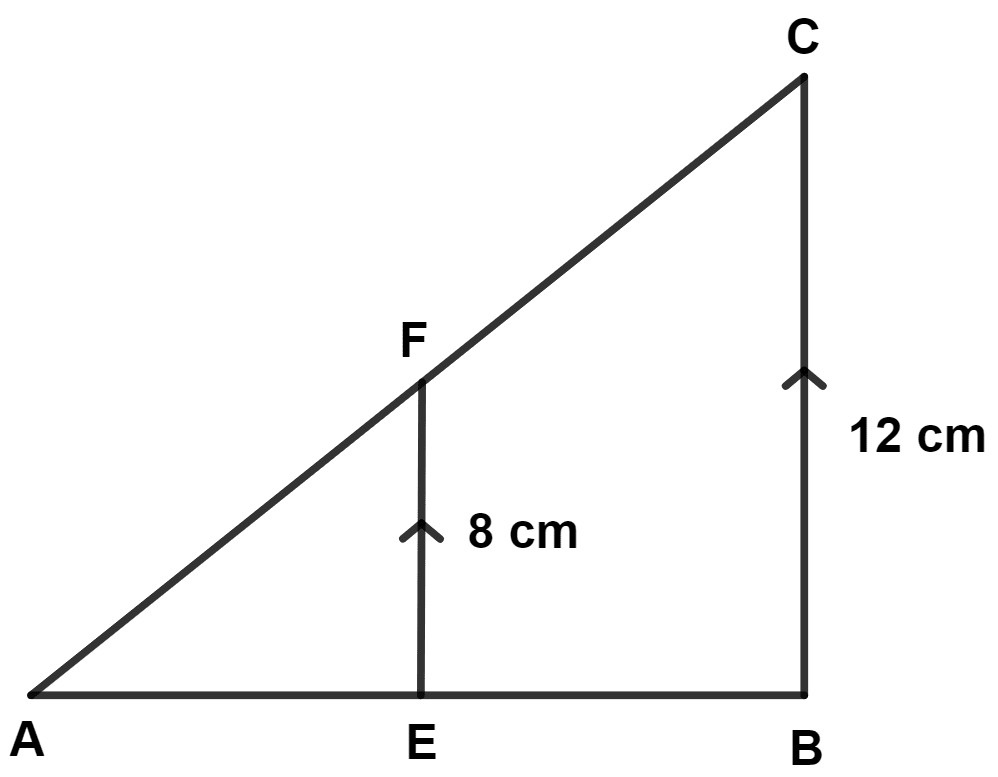
In the given figure, EF is parallel to BC. If area of triangle ABC is 576 cm2, the area of triangle AEF is :
128 cm2
288 cm2
256 cm2
768 cm2
