Mathematics
Triangle ABC is similar to triangle PQR. If AD and PM are altitudes of the two triangles, prove that: .
Similarity
7 Likes
Answer
Given, ∆ABC ~ ∆PQR
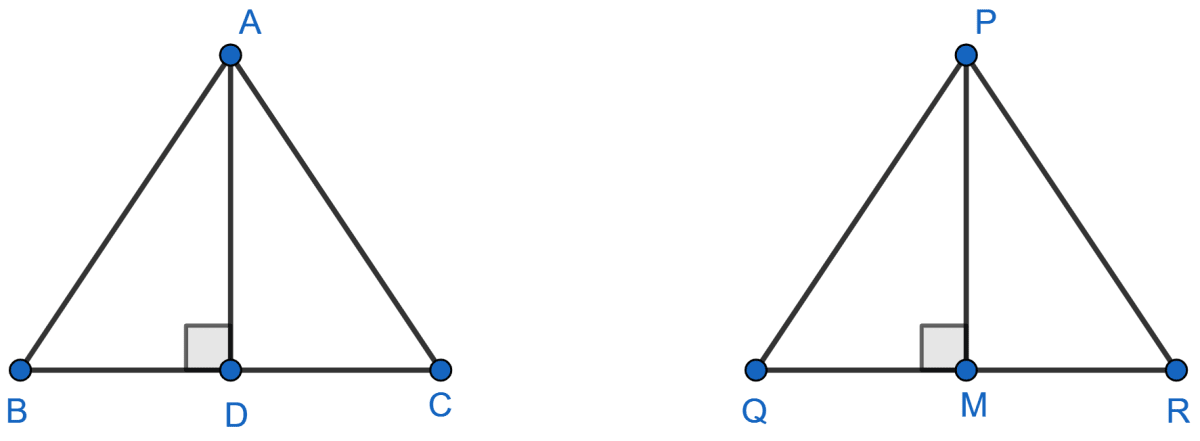
So,
∠ABC = ∠PQR i.e., ∠ABD = ∠PQM
Also, ∠ADB = ∠PMQ [Both are right angles]
∴ ∆ABD ~ ∆PQM [By AA]
Since, corresponding sides of similar triangles are proportional.
.
Hence, proved that .
Answered By
3 Likes
Related Questions
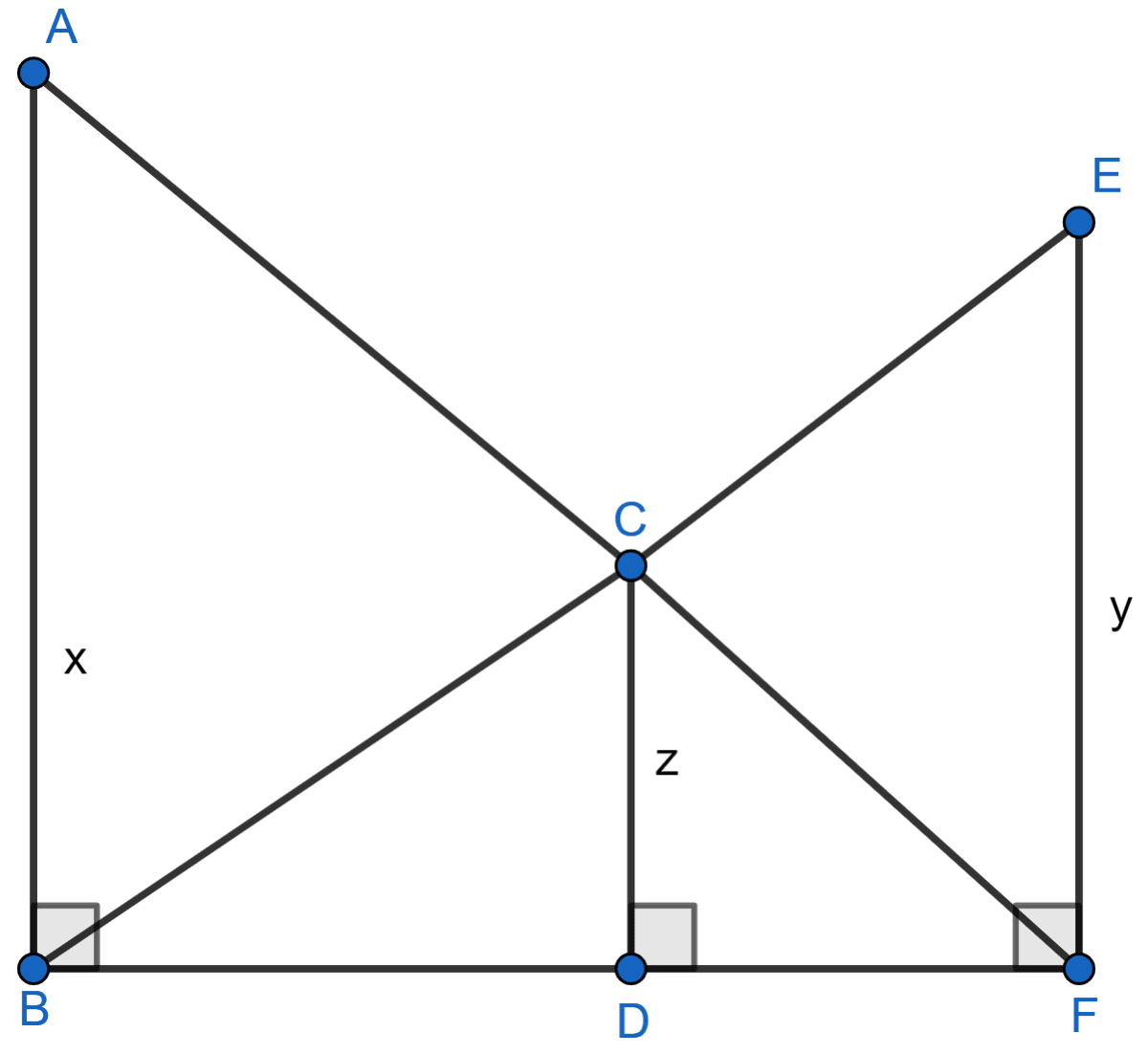
In the following figure, AB, CD and EF are perpendicular to the straight line BDF.
If AB = x and, CD = z unit and EF = y unit, prove that:
Triangle ABC is similar to triangle PQR. If AD and PM are corresponding medians of the two triangles, prove that: .
Triangle ABC is similar to triangle PQR. If bisector of angle BAC meets BC at point D and bisector of angle QPR meets QR at point M, prove that: .
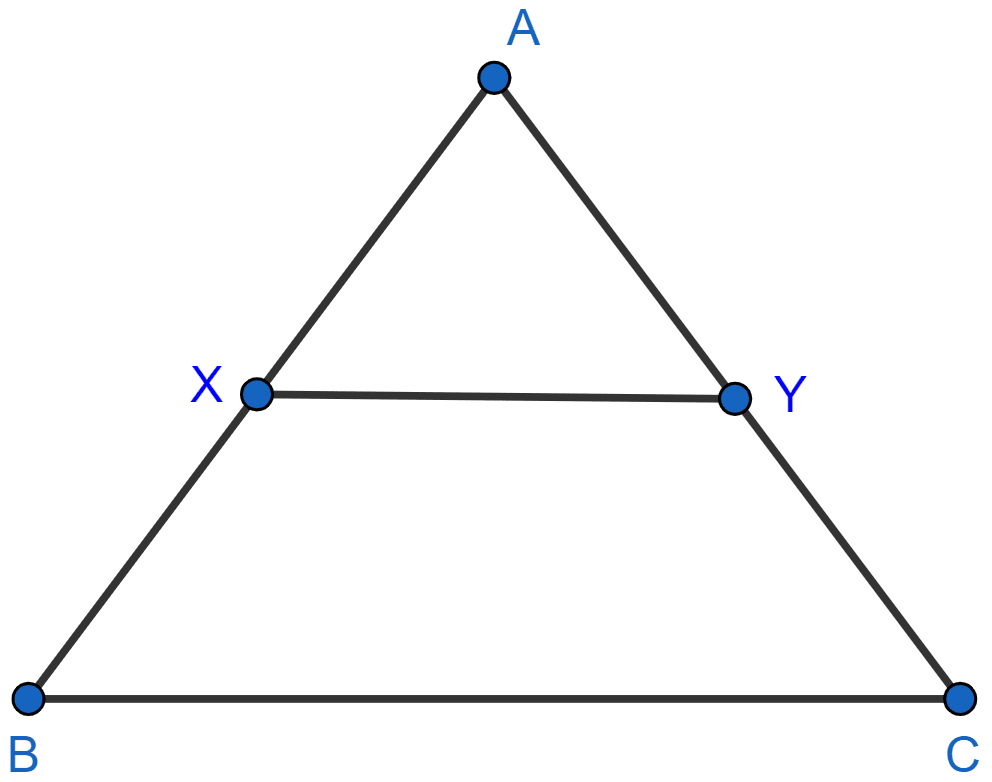
In the following figure, ∠AXY = ∠AYX.
If , show that triangle ABC is isosceles.