Mathematics
Three vertices of a rectangle are A(2, -1), B(2, 7) and C(4, 7). Plot these points on a graph and hence use it to find the co-ordinates of the fourth vertex D. Also find the co-ordinates of
(i) the mid-point of BC
(ii) the mid-point of CD
(iii) the point of intersection of the diagonals.
What is the area of the rectangle ?
Coordinate Geometry
3 Likes
Answer
In graph,
1 block = 1 unit.
Steps of construction :
Plot the points A(2, -1), B(2, 7) and C(4, 7) on graph.
Join AB and BC.
Measure AB. Draw a line segment CD, from point C parallel to y-axis.
Measure BC. Draw a line segment AD, from point A parallel to x-axis.
Mark F and G mid-point of BC and CD respectively.
Join AC and BD diagonals of rectangle.
Mark E as the point of intersection of diagonals.
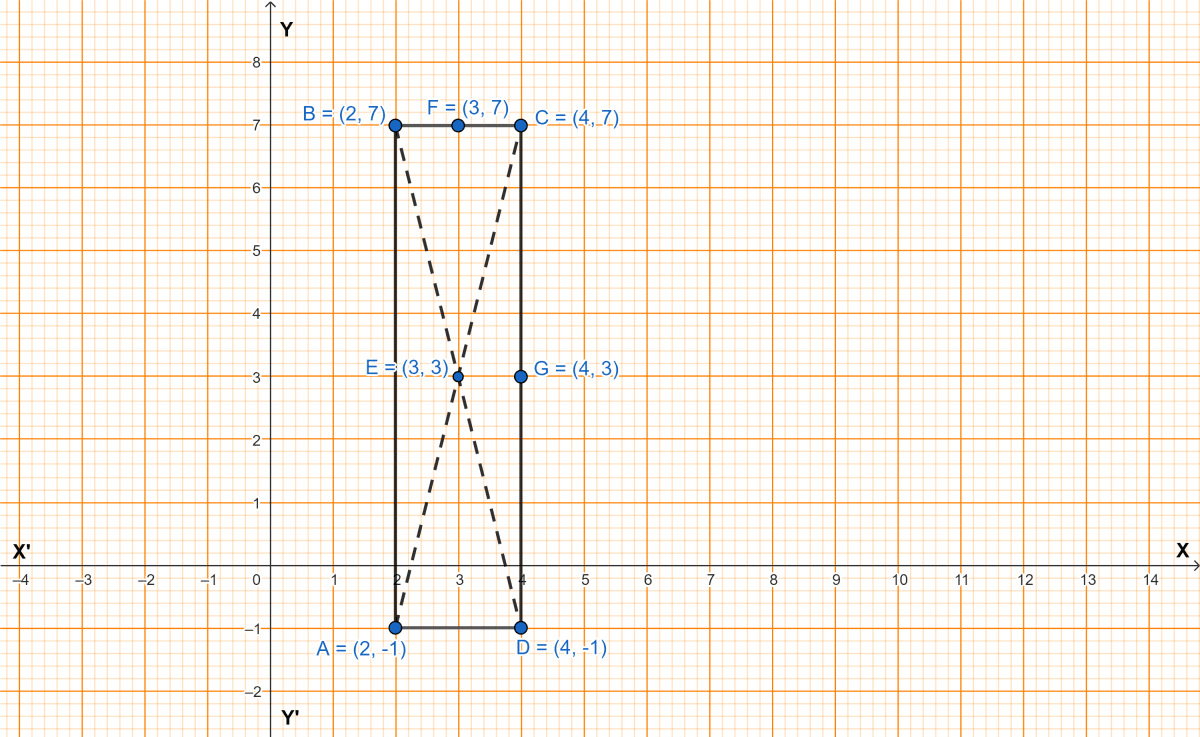
From graph,
Coordinates of D = (4, -1).
(i) From graph,
F is the mid-point of BC and F = (3, 7).
Hence, coordinates of mid-point of BC = (3, 7).
(ii) From graph,
G is the mid-point of CD and G = (4, 3).
Hence, coordinates of mid-point of CD = (4, 3).
(iii) From graph,
E is the point of intersection of diagonals.
Hence, point of intersection of the diagonals = (3, 3).
From graph,
AB = 8 units and BC = 2 units.
Area of the rectangle ABCD = length × breadth
= AB × BC
= 8 × 2
= 16 sq. units.
Hence, the area of the rectangle = 16 sq. units.
Answered By
1 Like
Related Questions
Three vertices of a parallelogram are A(3, 5), B(3, -1) and C(-1, -3). Plot these points on a graph paper and hence use it to find the coordinates of the fourth vertex D. Also find the coordinates of the mid-point of the side CD. What is the area of the parallelogram?
Draw the graphs of the following linear equation.
2x - 3y = 4
Also find slope and y-intercept of this line.
Draw the graphs of the following linear equation.
y = 2x - 1
Also find slope and y-intercept of this line.
Draw the graphs of the following linear equation.
2x + 3y = 6
Also find slope and y-intercept of this line.