Mathematics
Three vertices of a parallelogram are A(3, 5), B(3, -1) and C(-1, -3). Plot these points on a graph paper and hence use it to find the coordinates of the fourth vertex D. Also find the coordinates of the mid-point of the side CD. What is the area of the parallelogram?
Coordinate Geometry
5 Likes
Answer
Steps of construction :
Plot the points A(3, 5), B(3, -1) and C(-1, -3) on graph paper.
Join AB and BC.
From C draw a line CD parallel to AB, such that CD = AB.
From A draw a line AD parallel to BC, such that AD = BC.
Mark E, the mid-point of CD.
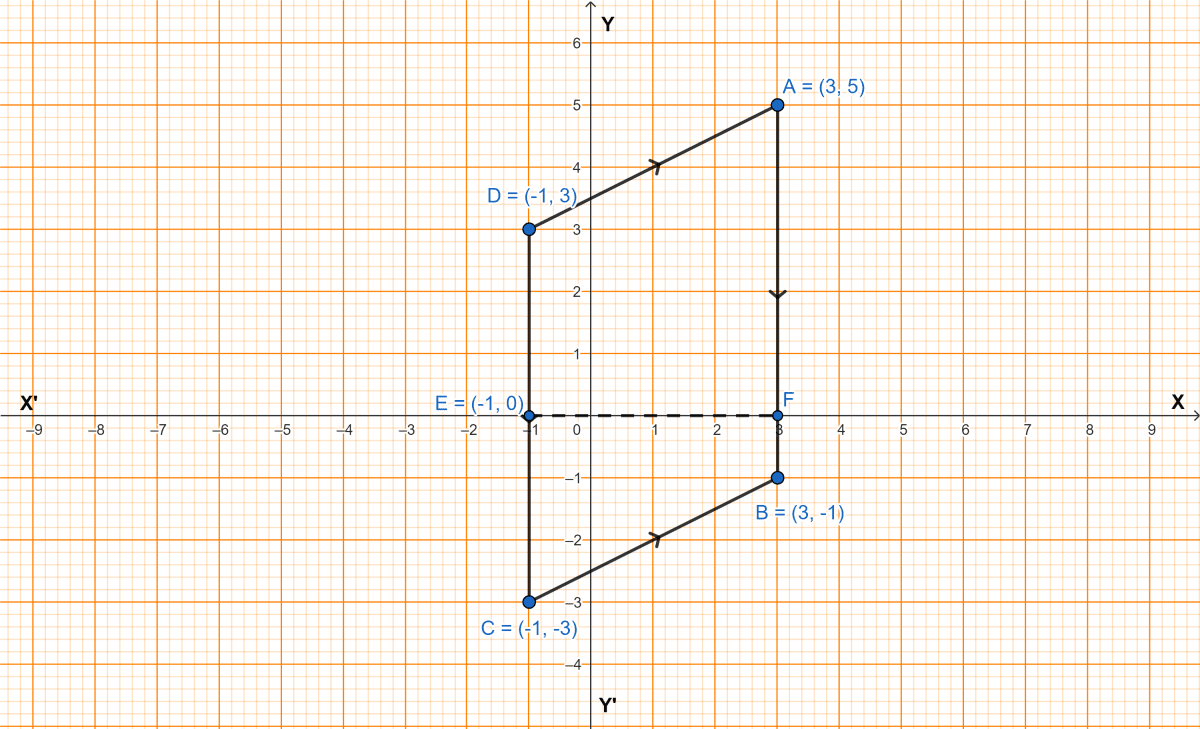
From graph,
The coordinates of fourth vertex D are (-1, 3).
The coordinates of the midpoint of CD i.e. E are (-1, 0).
As, 1 block = 1 unit
EF = 4 units
CD = 6 units
Area of parallelogram ABCD = Base × height
= CD × EF
= 6 × 4
= 24 sq. units.
Hence, D = (-1, 3), coordinates of mid-point of CD = (-1, 0) and the area of the parallelogram is 24 sq. units.
Answered By
3 Likes
Related Questions
Assertion (A): Point (0, 9) is a point on y-axis which is equidistant from points (6, 5) and (-4, 3).
Reason (R): Abscissa of a point on y-axis is 0.
Assertion (A) is true, Reason (R) is false.
Assertion (A) is false, Reason (R) is true.
Both Assertion (A) and Reason (R) are true, and Reason (R) is the correct reason for Assertion (A).
Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct reason (or explanation) for Assertion (A).
Three vertices of a rectangle are A(2, -1), B(2, 7) and C(4, 7). Plot these points on a graph and hence use it to find the co-ordinates of the fourth vertex D. Also find the co-ordinates of
(i) the mid-point of BC
(ii) the mid-point of CD
(iii) the point of intersection of the diagonals.
What is the area of the rectangle ?
Draw the graphs of the following linear equation.
y = 2x - 1
Also find slope and y-intercept of this line.
Draw the graphs of the following linear equation.
2x + 3y = 6
Also find slope and y-intercept of this line.