Mathematics
Three vertices of a rectangle are A(2, -1), B(2, 7) and C(4, 7). Plot these points on a graph and hence use it to find the co-ordinates of the fourth vertex D. Also find the co-ordinates of
(i) the mid-point of BC
(ii) the mid-point of CD
(iii) the point of intersection of the diagonals.
What is the area of the rectangle ?
Coordinate Geometry
6 Likes
Answer
In graph,
1 block = 1 unit.
Steps of construction :
Plot the points A(2, -1), B(2, 7) and C(4, 7) on graph.
Join AB and BC.
Measure AB. Draw a line segment CD, from point C parallel to y-axis.
Measure BC. Draw a line segment AD, from point A parallel to x-axis.
Mark F and G mid-point of BC and CD respectively.
Join AC and BD diagonals of rectangle.
Mark E as the point of intersection of diagonals.
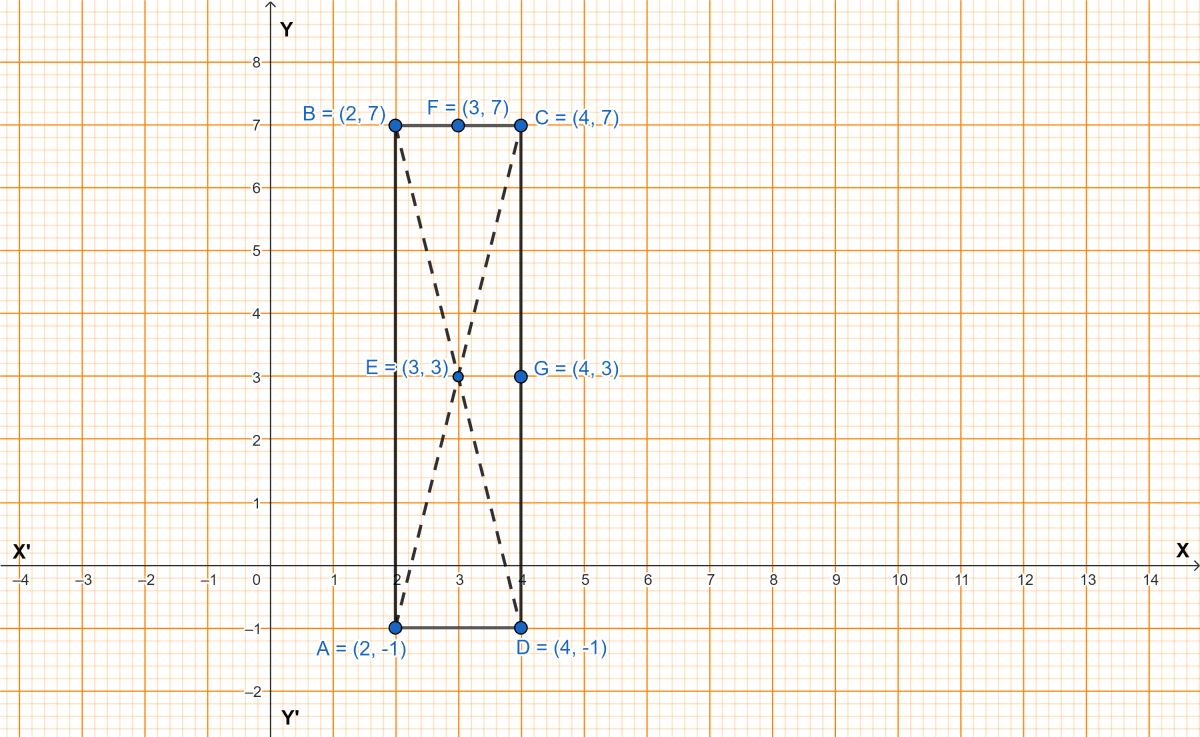
From graph,
Coordinates of D = (4, -1).
(i) From graph,
F is the mid-point of BC and F = (3, 7).
Hence, coordinates of mid-point of BC = (3, 7).
(ii) From graph,
G is the mid-point of CD and G = (4, 3).
Hence, coordinates of mid-point of CD = (4, 3).
(iii) From graph,
E is the point of intersection of diagonals.
Hence, point of intersection of the diagonals = (3, 3).
From graph,
AB = 8 units and BC = 2 units.
Area of the rectangle ABCD = length × breadth
= AB × BC
= 8 × 2
= 16 sq. units.
Hence, the area of the rectangle = 16 sq. units.
Answered By
2 Likes
Related Questions
Assertion (A): If the points A(2, 9), B(2, 5) and C(5, 5) are joined, then ΔABC is right angled.
Reason (R): If AC2 = AB2 + BC2, then ∠B = 90°.
Assertion (A) is true, Reason (R) is false.
Assertion (A) is false, Reason (R) is true.
Both Assertion (A) and Reason (R) are true, and Reason (R) is the correct reason for Assertion (A).
Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct reason (or explanation) for Assertion (A).
Assertion (A): Point (0, 9) is a point on y-axis which is equidistant from points (6, 5) and (-4, 3).
Reason (R): Abscissa of a point on y-axis is 0.
Assertion (A) is true, Reason (R) is false.
Assertion (A) is false, Reason (R) is true.
Both Assertion (A) and Reason (R) are true, and Reason (R) is the correct reason for Assertion (A).
Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct reason (or explanation) for Assertion (A).
Three vertices of a parallelogram are A(3, 5), B(3, -1) and C(-1, -3). Plot these points on a graph paper and hence use it to find the coordinates of the fourth vertex D. Also find the coordinates of the mid-point of the side CD. What is the area of the parallelogram?
Draw the graphs of the following linear equation.
y = 2x - 1
Also find slope and y-intercept of this line.