Physics
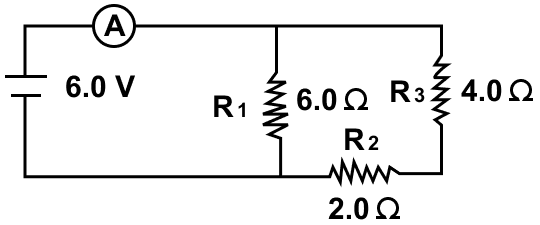
Three resistors of 6.0 Ω, 2.0 Ω and 4.0 Ω are joined to an ammeter A and a cell of e.m.f. 6.0 V as shown in figure. Calculate —
(a) the effective resistance of the circuit, and
(b) the reading of ammeter.
Current Electricity
25 Likes
Answer
In the circuit, there are two parts. In the first part, resistors of 2.0 and 4.0 Ω are connected in series. If the equivalent resistance of this part is Rs then
Rs = 2 + 4 = 6 Ω
In the second part, Rs = 6.0 and resistor of 6.0 Ω are connected in parallel. If the equivalent resistance of this part is Rp then
p} = \dfrac{1}{6} + \dfrac{1}{6} \\[0.5em] \dfrac{1}{Rp} = \dfrac{1 + 1}{6} \\[0.5em] \dfrac{1}{Rp} = \dfrac{2}{6} \\[0.5em] Rp = \dfrac{6}{2} \\[0.5em] R_p = 3.0 Ω \\[0.5em]
Hence, the effective resistance of the circuit = 3 Ω
(b) The reading of ammeter = ?
R = 3 Ω
V = 6.0 V
Using Ohm's law,
V = IR
Substituting the values in the formula above we get,
6 = I x 3
⇒ I = 6 / 3 = 2 A
Hence, the reading of ammeter = 2 A
Answered By
15 Likes
Related Questions
A battery of e.m.f. 16 V and internal resistance 2 Ω is connected to two resistors 3 Ω and 6 Ω connected in parallel. Find (a) the current through the battery (b) p.d. between the terminals of the battery (c) the current in 3 Ω resistor (d) the current in 6 Ω resistor.
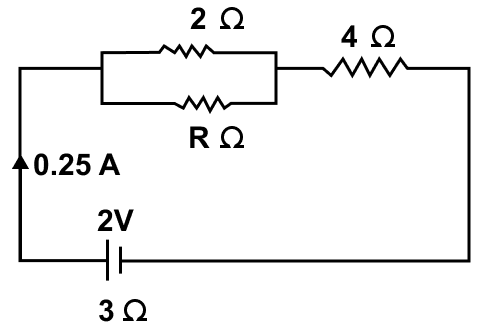
The circuit diagram in figure shows three resistors 2 Ω, 4 Ω and R Ω connected to a battery of e.m.f. 2V and internal resistance 3 Ω. If main current of 0.25 A flows through the circuit, find —
(a) the p.d. across the 4 Ω resistor
(b) the p.d. across the internal resistance of the cell,
(c) the p.d. across the R Ω or 2 Ω resistor, and
(d) the value of R.
The diagram below in figure shows the arrangement of five different resistances connected to a battery of e.m.f. 1.8 V. Calculate —
(a) the total resistance of the circuit, and
(b) the reading of ammeter A.

A cell of e.m.f. 2 V and internal resistance 1.2 Ω is connected to an ammeter of resistance 0.8 Ω and two resistors of 4.5 Ω and 9 Ω as shown in figure.
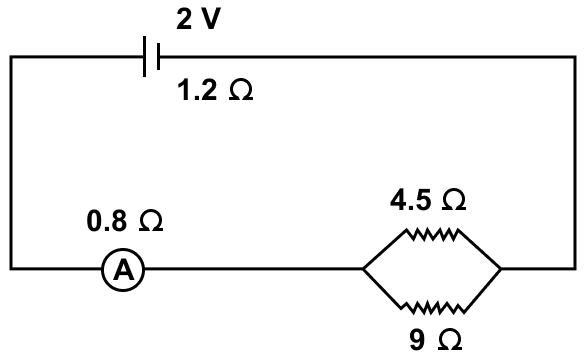
Find —
(a) the reading of the ammeter,
(b) the potential difference across the terminals of the cell, and
(c) the potential difference across the 4.5 Ω resistor.