Physics
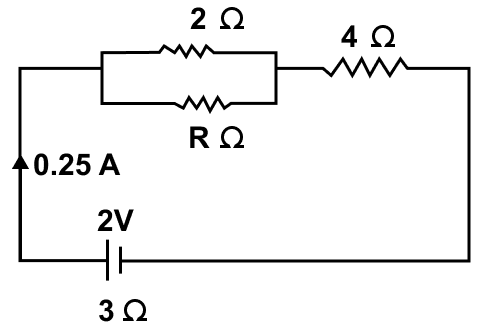
The circuit diagram in figure shows three resistors 2 Ω, 4 Ω and R Ω connected to a battery of e.m.f. 2V and internal resistance 3 Ω. If main current of 0.25 A flows through the circuit, find —
(a) the p.d. across the 4 Ω resistor
(b) the p.d. across the internal resistance of the cell,
(c) the p.d. across the R Ω or 2 Ω resistor, and
(d) the value of R.
Current Electricity
114 Likes
Answer
(a) Given,
resistor = 4 Ω
I = 0.25 A
the p.d. across the 4 Ω resistor (V) = ?
Using Ohm's law
V = IR
Substituting the values in the formula above we get,
V = 0.25 x 4 = 1 V
Hence, the p.d. across the 4 Ω resistor (V) = 1 V
(b) Given,
internal resistance = 3 Ω
I = 0.25 A
the p.d. across the internal resistance of the cell = ?
Using Ohm's law
V = IR
Substituting the values in the formula above we get,
V = 0.25 x 3 = 0.75 V
Hence, the p.d. across the internal resistance (V) = 0.75 V
(c) Potential difference across R Ω or 2 Ω
V = Vnet - Vacross 4 Ω - Vacross 3 Ω
Hence, we get,
V = 2 - 1 - 0.75 = 0.25 V
(d) The p.d. across resistor of R Ω = 0.25 V
Let the equivalent resistance of the resistors of 2 Ω and R Ω connected in parallel be R'p
p} = \dfrac{1}{R} + \dfrac{1}{2} \\[0.5em] \Rightarrow \dfrac{1}{R'p} = \dfrac{2 + R}{2R} \\[0.5em] \Rightarrow R'_p = \dfrac{2R}{2 + R} \\[0.5em]
Using Ohm's law
V = IR
0.25 = 0.25 x R'p
Substituting the value of R'p from above:
Hence, value of R = 2 Ω
Answered By
73 Likes
Related Questions
A cell supplies a current of 1.2 A through two resistors each of 2 Ω connected in parallel. When the resistors are connected in series, it supplies a current of 0.4 A. Calculate (i) the internal resistance and (ii) e.m.f. of the cell.
A battery of e.m.f. 16 V and internal resistance 2 Ω is connected to two resistors 3 Ω and 6 Ω connected in parallel. Find (a) the current through the battery (b) p.d. between the terminals of the battery (c) the current in 3 Ω resistor (d) the current in 6 Ω resistor.
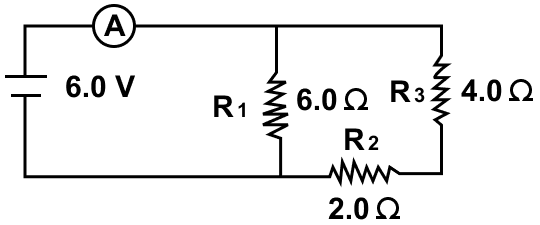
Three resistors of 6.0 Ω, 2.0 Ω and 4.0 Ω are joined to an ammeter A and a cell of e.m.f. 6.0 V as shown in figure. Calculate —
(a) the effective resistance of the circuit, and
(b) the reading of ammeter.
The diagram below in figure shows the arrangement of five different resistances connected to a battery of e.m.f. 1.8 V. Calculate —
(a) the total resistance of the circuit, and
(b) the reading of ammeter A.
