Physics
A cell of e.m.f. 2 V and internal resistance 1.2 Ω is connected to an ammeter of resistance 0.8 Ω and two resistors of 4.5 Ω and 9 Ω as shown in figure.
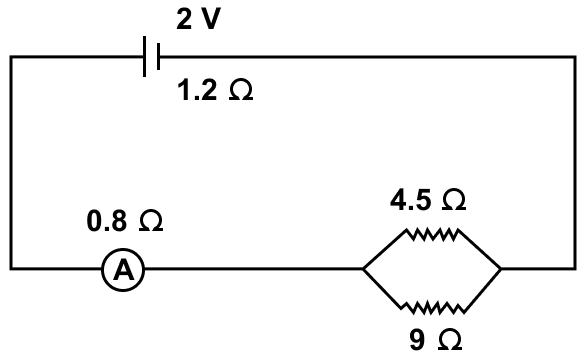
Find —
(a) the reading of the ammeter,
(b) the potential difference across the terminals of the cell, and
(c) the potential difference across the 4.5 Ω resistor.
Current Electricity
83 Likes
Answer
Given,
e.m.f. = 2V
I = ?
In the circuit, there are two parts. In the first part, resistors of 4.5 Ω and 9 Ω are connected in parallel. If the equivalent resistance of this part is Rp then
p} = \dfrac{1}{4.5} + \dfrac{1}{9} \\[0.5em] \dfrac{1}{Rp} = \dfrac{9 + 4.5}{4.5 \times 9} \\[0.5em] \dfrac{1}{Rp} = \dfrac{13.5}{40.5} \\[0.5em] Rp = \dfrac{40.5}{13.5} \\[0.5em] R_p = 3 Ω \\[0.5em]
In the second part, 1.2 Ω, 0.8 Ω and Rp = 3 Ω are connected in series. If the equivalent resistance of this part is Rs then
s = 1.2 + 0.8 + 3 \\[0.5em] Rs = 5 Ω \\[0.5em]
Hence, the effective resistance of the circuit = 5 Ω
Using Ohm's law,
V = IR
Hence, the reading of the ammeter = 0.4 A
(b) The potential difference across the ends of the cells = ?
ε = 2 V
I = 0.4 A
r = 1.2 Ω
From relation,
Voltage (V) = ε – Ir
Substituting the values in the formula we get,
Hence, potential difference across the terminals of the cell = 1.52 V
(c) The potential difference across the 4.5 Ω resistor = ?
Current flowing is I = 0.4 A. Now the current I divides in two parts. Let the current in 4.5 Ω resistor be I1 and in 9 Ω resistor be I2.
So I = I1 + I2
and I1 x 4.5 = I2 x 9
On solving,
1 = \dfrac{9}{4.5 + 9} \times I \\[0.5em] I1 = \dfrac{9}{4.5 + 9} \times 0.4 \\[0.5em] I_1 = 0.2667 \\[0.5em]
p.d. across the 4.5 Ω resistor
Alternate Method:
V4.5Ω = Vcell - Vammeter
{4.5Ω} = 1.52 - IR \\[0.5em] V{4.5Ω} = 1.52 - (0.4 \times 0.8) \\[0.5em] V{4.5Ω} = 1.52 - 0.32 \\[0.5em] V{4.5Ω} = 1.2 V
Hence, p.d. across the 4.5 Ω resistor = 1.2 V
Answered By
56 Likes
Related Questions
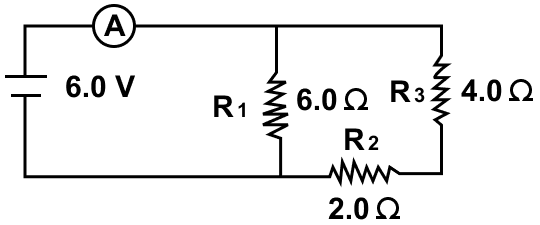
Three resistors of 6.0 Ω, 2.0 Ω and 4.0 Ω are joined to an ammeter A and a cell of e.m.f. 6.0 V as shown in figure. Calculate —
(a) the effective resistance of the circuit, and
(b) the reading of ammeter.
The diagram below in figure shows the arrangement of five different resistances connected to a battery of e.m.f. 1.8 V. Calculate —
(a) the total resistance of the circuit, and
(b) the reading of ammeter A.

The electrical energy supplied by a source is given by:
- W = QV
- W = VIt
- W = I2Rt
- All of the above
The S.I. unit of electrical power is :
- volt x ampere
- volt/ampere
- joule x second
- none of the above