Mathematics
The speed of a boat in still water is 11 km per hour. It can go 12 km upstream and return downstream to the original point in 2 hours and 45 minutes. Find the speed of stream.
Quadratic Equations
3 Likes
Answer
Given,
Speed of boat = 11 km/hour
Let speed of stream be x km/hour.
Speed of boat (upstream) = (11 - x) km/hour
Speed of boat (downstream) = (11 + x) km/hour
Distance covered = 24 km (12 + 12)
Time taken = 2 hours 45 minutes = hours
By formula,
Time =
Since, boat goes 12 km upstream and 12 km downstream.
Since, speed cannot be negative.
∴ Speed of stream = 5 km/hour.
Hence, speed of stream = 5 km/hour.
Answered By
1 Like
Related Questions
Solve :
13x - 5 < 15x + 4 < 7x + 12, x ∈ R. Represent the solution set on a real number line.
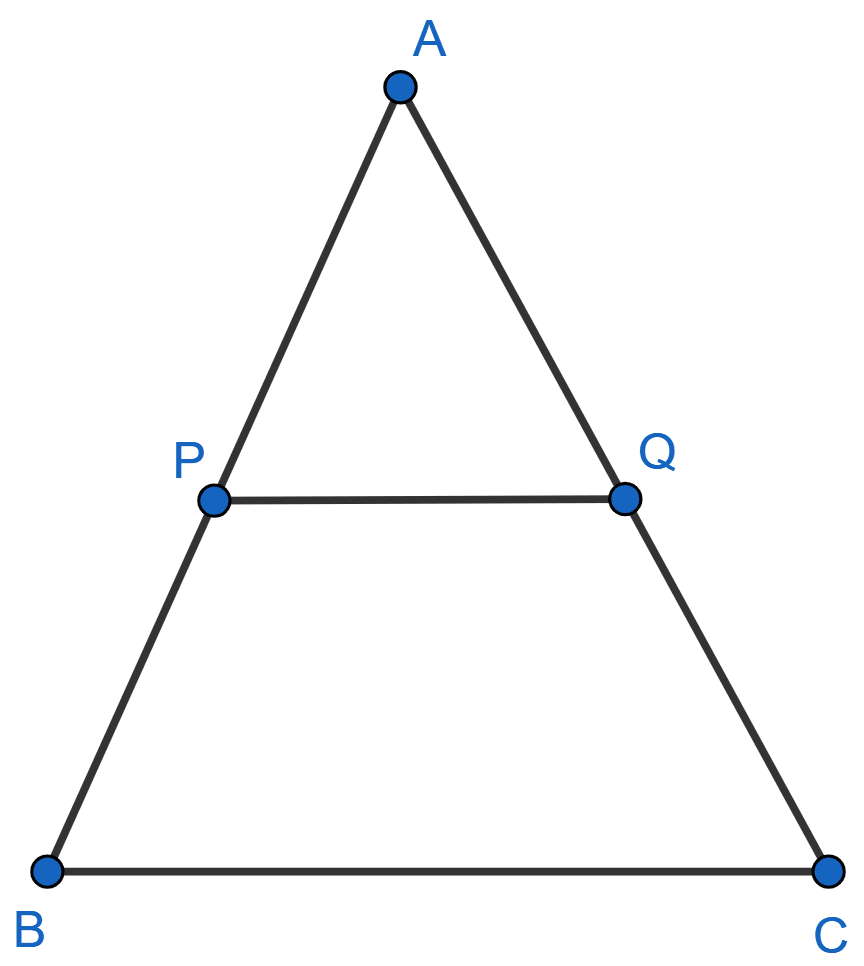
P and Q are points on the sides AB and AC of triangle ABC. If AP = 3 cm, PB = 6 cm, AQ = 4.5 cm and QC = 9 cm, show that BC = 3 × PQ.
The marks obtained (out of 100) by 400 students in an examination are given below :
Marks No. of students 0-10 10 10-20 20 20-30 22 30-40 40 40-50 54 50-60 76 60-70 80 70-80 58 80-90 28 90-100 12 Using a graph paper, draw an ogive for the above distribution. Use your graph to estimate :
(i) the median marks.
(ii) the number of students who obtained more than 80% marks in the examination.
(iii) the number of students who did not pass, if the pass percentage was 35.
If , prove that :
(i) a : b = c : d
(ii)