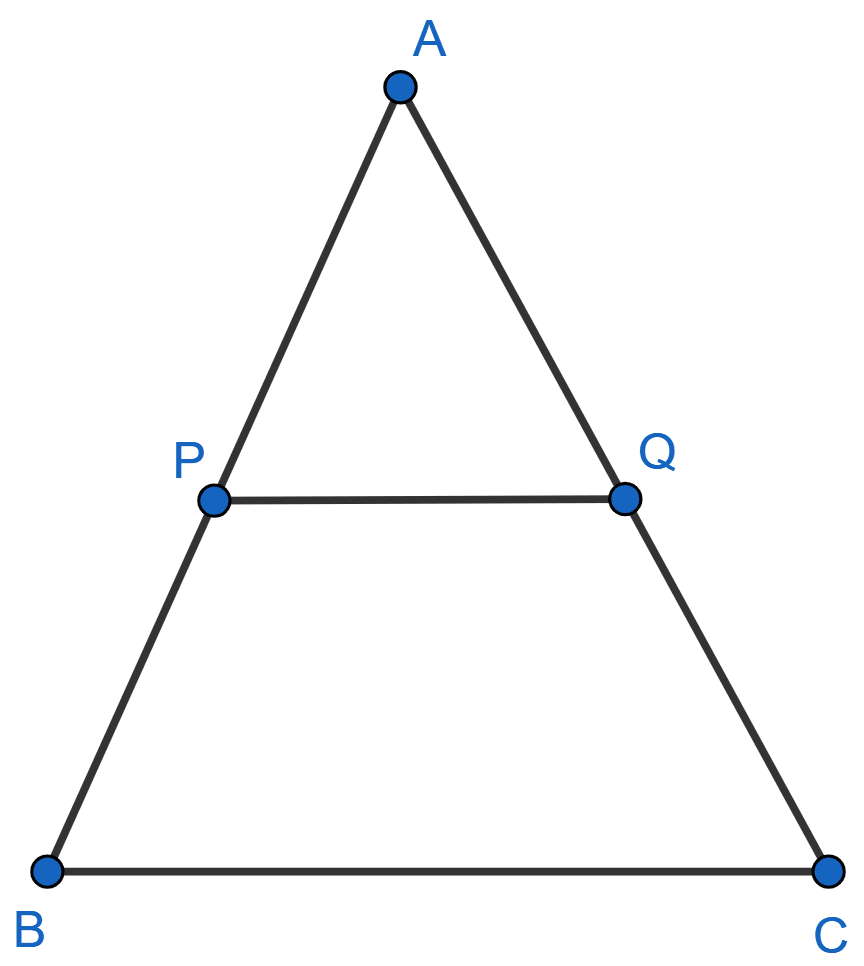
P and Q are points on the sides AB and AC of triangle ABC. If AP = 3 cm, PB = 6 cm, AQ = 4.5 cm and QC = 9 cm, show that BC = 3 × PQ.

Calculating,

$\dfrac{AP}{PB} = \dfrac{3}{6} = \dfrac{1}{2}$

$\dfrac{AQ}{QC} = \dfrac{4.5}{9} = \dfrac{1}{2}$.

So,

$\dfrac{AP}{PB} = \dfrac{AQ}{QC}$.

∴ PQ || BC (By converse of basic proportionality theorem)

In Δ APQ and Δ ABC

∠APQ = ∠ABC (corresponding angles are equal)

∠AQP = ∠ACB (corresponding angles are equal)

∴ Δ APQ ~ Δ ABC (By A.A. axiom)

From figure,

AB = AP + PB = 3 + 6 = 9 cm.

We know that,

In similar triangles ratio of corresponding sides are proportional.

$\Rightarrow \dfrac{AP}{AB} = \dfrac{PQ}{BC} \\[1em] \Rightarrow \dfrac{3}{9} = \dfrac{PQ}{BC} \\[1em] \Rightarrow \dfrac{1}{3} = \dfrac{PQ}{BC} \\[1em] \Rightarrow BC = 3 \times PQ.$

Hence, proved that BC = 3 × PQ.