Mathematics
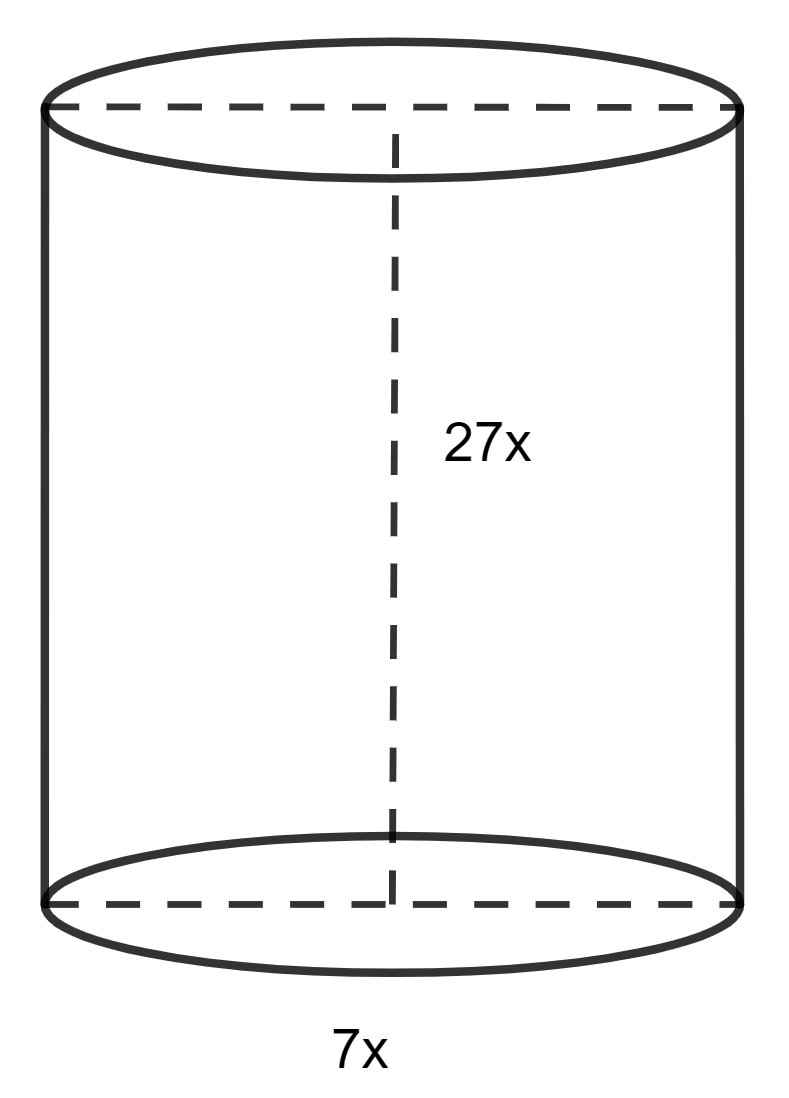
The ratio of the radius and the height of a solid metallic right circular cylinder is 7 : 27. This is melted and made into a cone of diameter 14 cm and slant height 25 cm. Find the height of the :
(a) cone
(b) cylinder
Mensuration
28 Likes
Answer
Given,
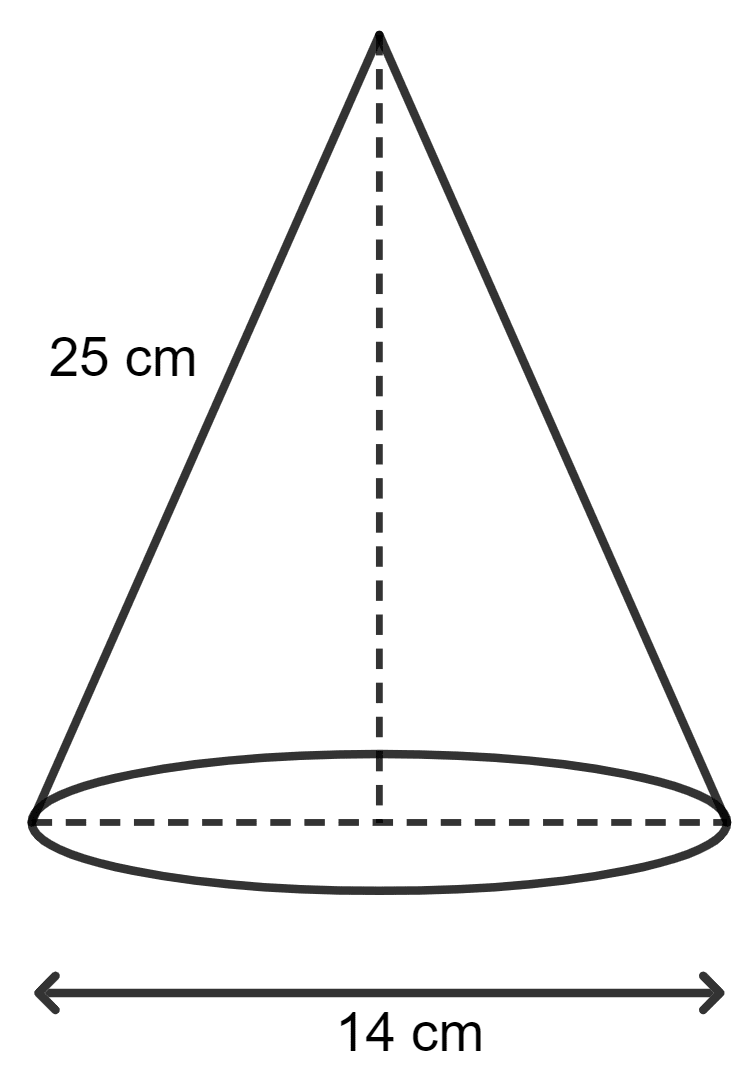
Diameter of cone = 14 cm
Radius of cone (r) = = 7 cm
Slant height (l) = 25 cm
Ratio of the radius and the height of a solid metallic right circular cylinder is 7 : 27.
Radius of cylinder (R) = 7x
Height of cylinder (H) = 27x
(a) Let height of cone be h cm.
By formula,
⇒ l2 = r2 + h2
⇒ 252 = 72 + h2
⇒ 625 = 49 + h2
⇒ h2 = 625 - 49
⇒ h2 = 576
⇒ h = = 24 cm.
Hence, height of cone = 24 cm.
(b) Given,
A solid metallic right circular cylinder is melted and made into a cone.
∴ Volume of cylinder = Volume of cone
⇒ πR2H =
⇒ R2H =
⇒ (7x)2 × 27x =
⇒ 1323x3 =
⇒ 1323x3 = 392
⇒ x3 =
⇒ x3 =
⇒ x3 =
⇒ x =
Height of cylinder (H) = 27x = = 18 cm.
Hence, height of cylinder = 18 cm.
Answered By
21 Likes
Related Questions
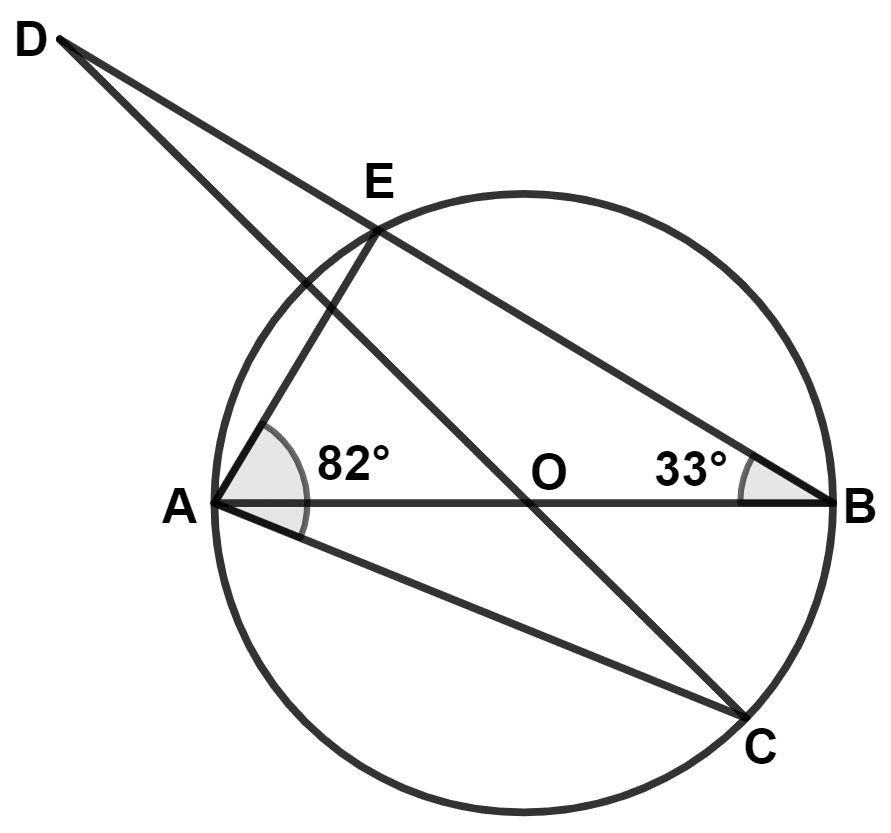
AB and CD intersect at the center O of the circle given in the above diagram. If ∠EBA = 33° and ∠EAC = 82°, find
(a) ∠BAE
(b) ∠BOC
(c) ∠ODB
A famous sweet shop “Madanlal Sweets” sells tinned rasgullas. The tin container is cylindrical in shape with diameter 14 cm, height 16 cm, and it can hold 20 spherical rasgullas of diameter 6 cm and sweetened liquid such that the can is filled and then sealed. Find out how much sweetened liquid the can contains. Take π = 3.14.
An inclined plane AC is prepared with its base AB which is √3 times its vertical height BC. The length of the inclined plane is 15 m. Find:
(a) value of θ.
(b) length of its base AB, in nearest metre.
Prove that :
tan2 θ + cos2 θ - 1 = tan2 θ. sin2 θ