Mathematics
Prove that :
tan2 θ + cos2 θ - 1 = tan2 θ. sin2 θ
Trigonometric Identities
7 Likes
Answer
Solving L.H.S. of the above equation, we get :
⇒ tan2 θ + cos2 θ - 1
⇒ - (1 - cos2 θ)
⇒ - sin2 θ
⇒ sin2 θ
⇒
⇒ . sin2 θ
⇒ tan2 θ. sin2 θ.
Since. L.H.S. = R.H.S.
Hence, proved that tan2 θ + cos2 θ - 1 = tan2 θ. sin2 θ
Answered By
3 Likes
Related Questions
The ratio of the radius and the height of a solid metallic right circular cylinder is 7 : 27. This is melted and made into a cone of diameter 14 cm and slant height 25 cm. Find the height of the :
(a) cone
(b) cylinder
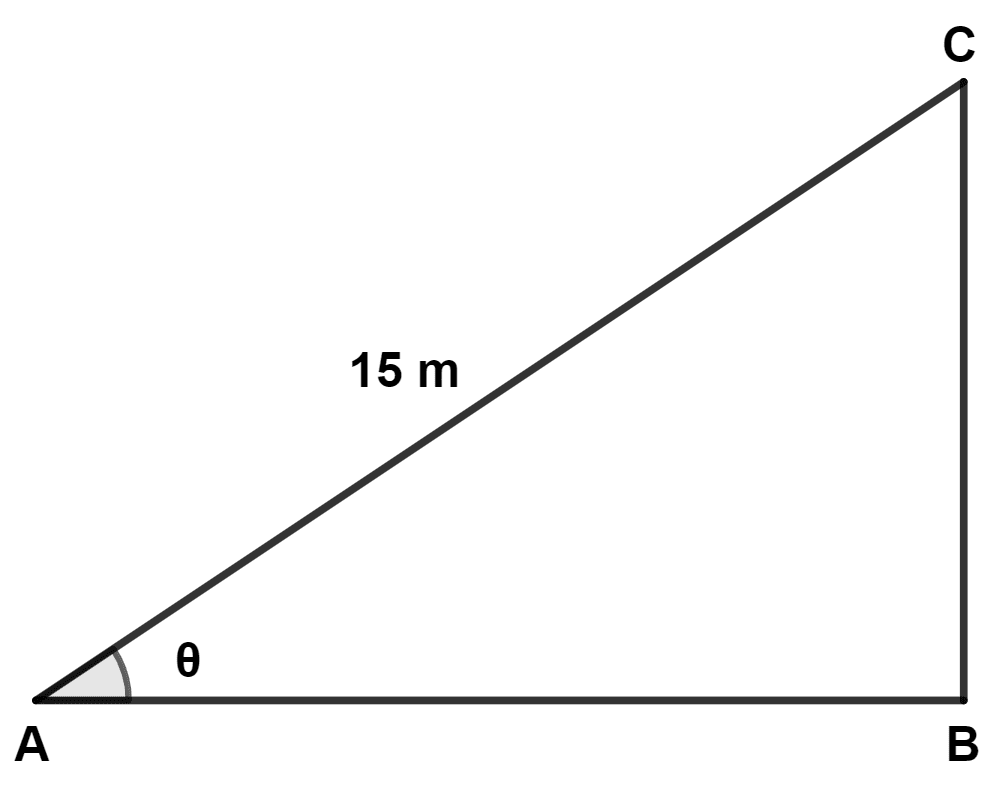
An inclined plane AC is prepared with its base AB which is √3 times its vertical height BC. The length of the inclined plane is 15 m. Find:
(a) value of θ.
(b) length of its base AB, in nearest metre.
The class mark and frequency of a data is given in the graph. From the graph, Find:
(a) the table showing the class interval and frequency.
(b) the mean

The mean of 5, 7, 8, 4 and m is n and the mean of 5, 7, 8, 4, m and n is m. Find the values of m and n.