Mathematics
The radii of two concentric circles are 6 cm and 10 cm respectively. Find the length of the chord of the bigger circle which is tangent to smaller circle.
Circles
3 Likes
Answer
From figure,
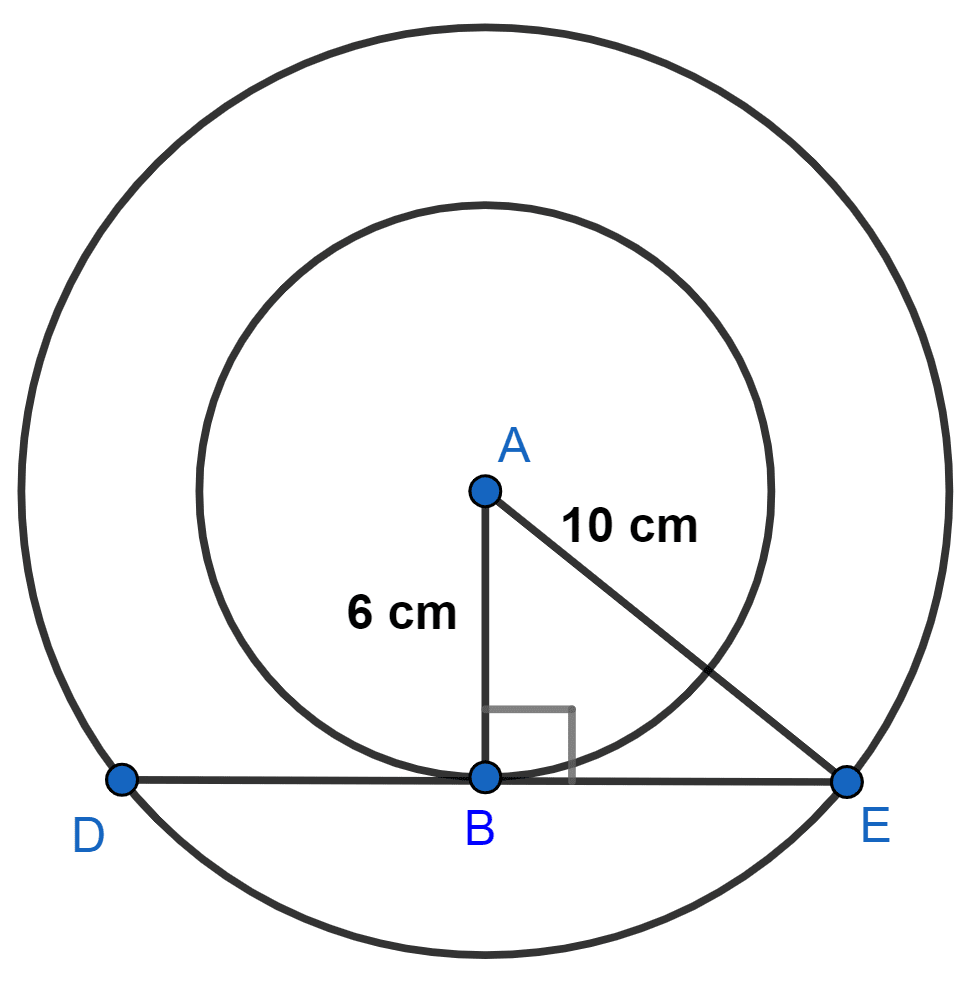
There are two circles with center A and radius AE = 10 cm and AB = 6 cm.
In △ABE,
⇒ AE2 = AB2 + BE2
⇒ 102 = 62 + BE2
⇒ 100 = 36 + BE2
⇒ BE2 = 100 - 36
⇒ BE2 = 64
⇒ BE = = 8 cm.
We know that,
The perpendicular from the centre to a chord bisect the chord.
DE = 2BE = 2 × 8 = 16 cm.
Hence, length of chord of bigger circle which is tangent to smaller circle = 16 cm.
Answered By
2 Likes
Related Questions
The following table shows the marks obtained (out of 100) by different students of class X.
Marks No. of students 50-60 8 60-70 16 70-80 28 80-90 38 90-100 10 Taking suitable scales on both the axes, draw a histogram and use it to estimate mode.
If matrix M = }[r] 3 & -2 \ 4 & -2 \end{bmatrix}, find M2 + 3I.
If x2 - 3x + 2 is a factor of x3 - ax2 + b, find the values of a and b.
In the given figure, P(-3, -4) is the mid-point of the line segment AB.
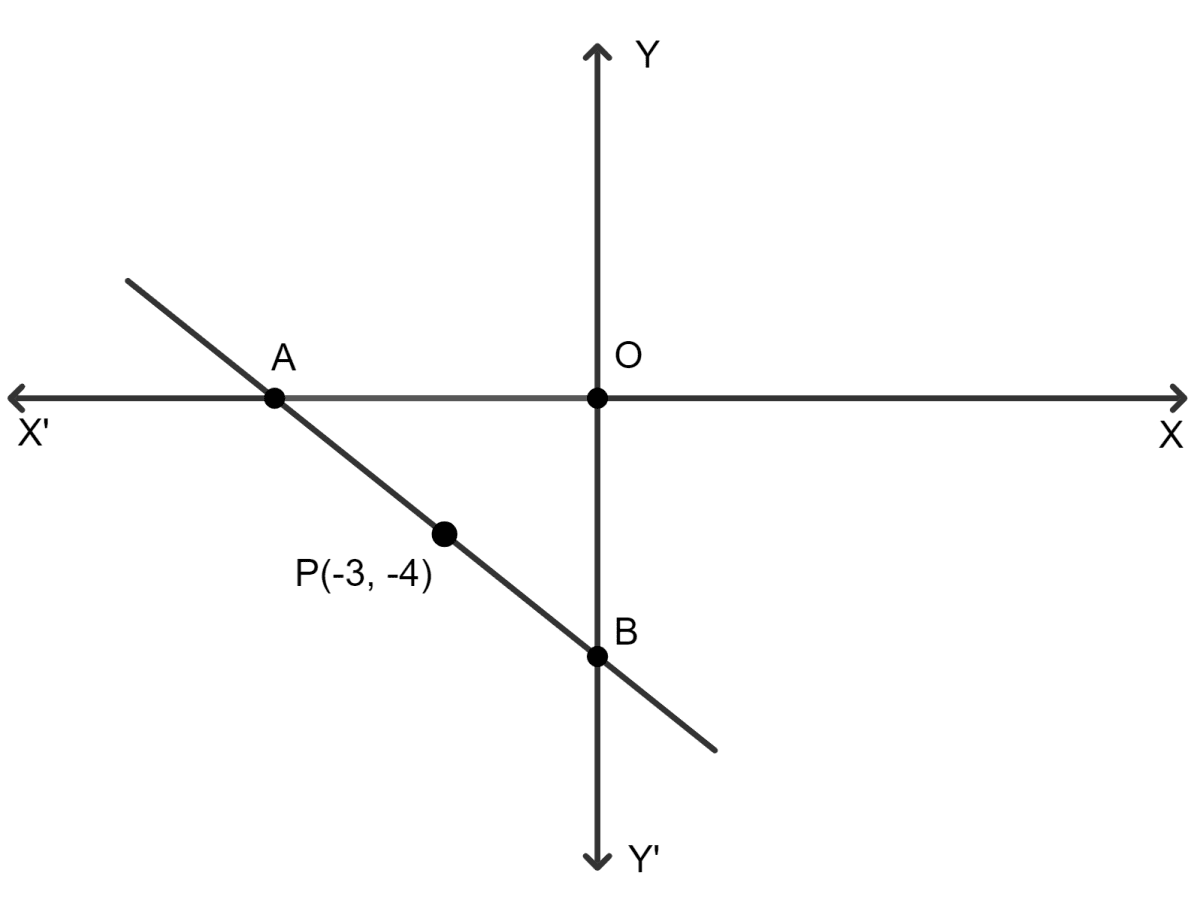
Find the coordinates of points A and B. Also, find the equation of the line passing through the point P and also perpendicular to line-segment AB.