In the given figure, P(-3, -4) is the mid-point of the line segment AB.

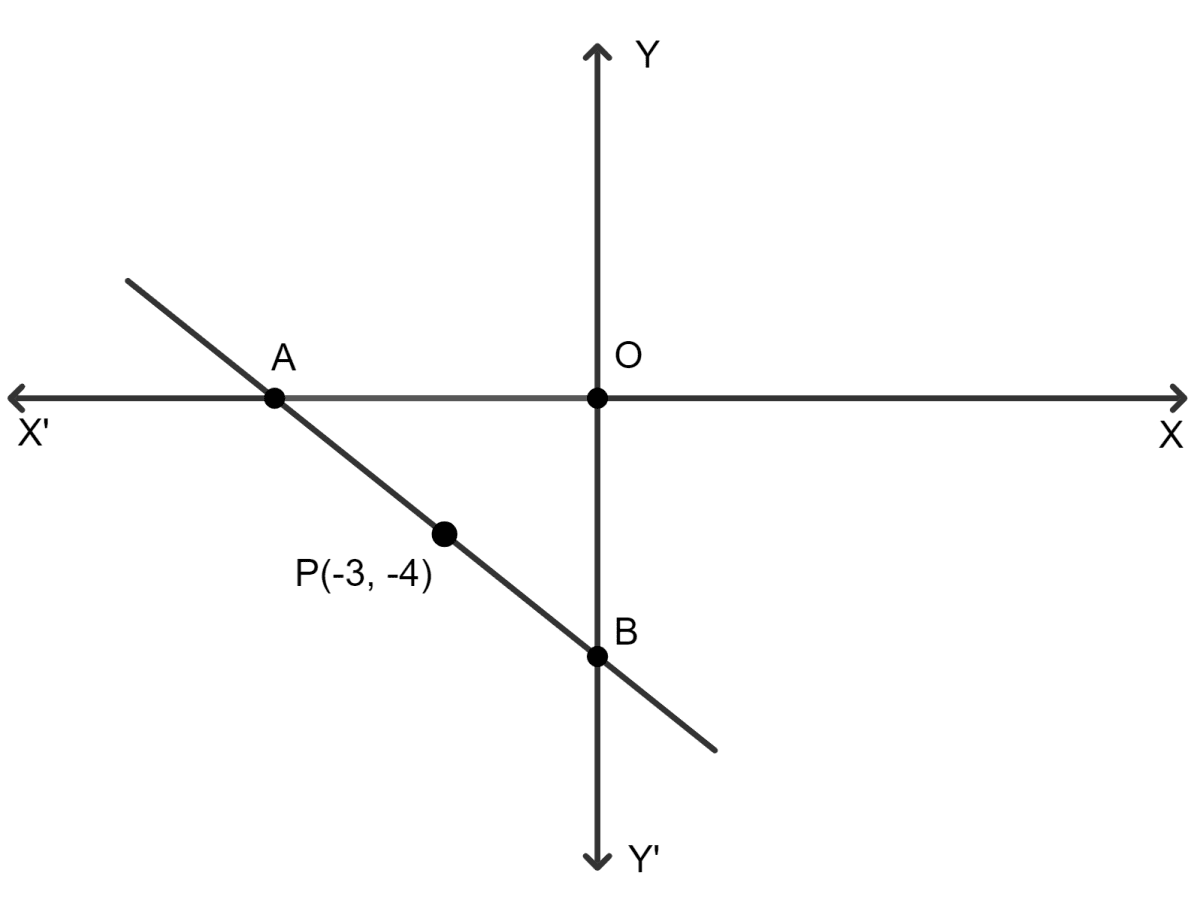
Find the coordinates of points A and B. Also, find the equation of the line passing through the point P and also perpendicular to line-segment AB.

From figure,

A lies on x-axis and B lies on y-axis.

Let coordinates of

A = (a, 0) and B = (0, b).

By mid-point formula,

M = $\Big(\dfrac{x$1 + x2}{2}, \dfrac{y1 + y2}{2}\Big)

As P is the mid-point of AB,

⇒ P = $\Big(\dfrac{a + 0}{2}, \dfrac{0 + b}{2}\Big)$

⇒ (-3, -4) = $\Big(\dfrac{a}{2}, \dfrac{b}{2}\Big)$

⇒ $\dfrac{a}{2} = -3 \text{ and } \dfrac{b}{2} = -4$

⇒ a = -6 and b = -8.

A = (-6, 0) and B = (0, -8).

By formula,

Slope = $\dfrac{y$2 - y1}{x2 - x1}

Slope of AB = $\dfrac{-8 - 0}{0 - (-6)} = -\dfrac{8}{6} = -\dfrac{4}{3}$.

We know that,

Product of slope of perpendicular lines = -1.

∴ Slope of AB × Slope of line perpendicular to AB (m) = -1

⇒ $-\dfrac{4}{3} \times m = -1$

⇒ m = $\dfrac{-3}{-4} = \dfrac{3}{4}$.

By point-slope form,

Equation of line is y - y₁ = m(x - x₁)

Substituting values we get :

Equation of line passing through P and slope = $\dfrac{3}{4}$ is

⇒ y - y₁ = m(x - x₁)

⇒ y - (-4) = $\dfrac{3}{4}$[x - (-3)]

⇒ 4(y + 4) = 3(x + 3)

⇒ 4y + 16 = 3x + 9

⇒ 3x - 4y + 9 - 16 = 0

⇒ 3x - 4y - 7 = 0

⇒ 4y = 3x - 7.

Hence, A = (-6, 0) and B = (0, -8) and equation of line passing through the point P and also perpendicular to line-segment AB is 4y = 3x - 7.