Mathematics
If the 3rd and the 9th terms of an arithmetic progression are 4 and -8 respectively. Which term of it is zero ?
AP GP
2 Likes
Answer
Let first term be a and common difference be d.
Given,
⇒ 3rd term = 4
⇒ a3 = 4
⇒ a + 2d = 4
⇒ a = 4 - 2d ……..(Eq. 1)
Given,
⇒ 9th term = -8
⇒ a9 = -8
⇒ a + 8d = -8
⇒ a = -8 - 8d ……..(Eq. 2)
From Eq. 1 and Eq. 2,
⇒ 4 - 2d = -8 - 8d
⇒ -2d + 8d = -8 - 4
⇒ 6d = -12
⇒ d = = -2.
Substituting value of d in Eq. 1, we get :
⇒ a = 4 - 2d = 4 - 2(-2) = 4 + 4 = 8.
Let nth term be zero.
⇒ an = 0
⇒ a + (n - 1)d = 0
⇒ 8 + (n - 1)(-2) = 0
⇒ 8 - 2n + 2 = 0
⇒ 2n = 10
⇒ n = = 5.
Hence, 5th term will be 0.
Answered By
1 Like
Related Questions
In the given figure, P(-3, -4) is the mid-point of the line segment AB.
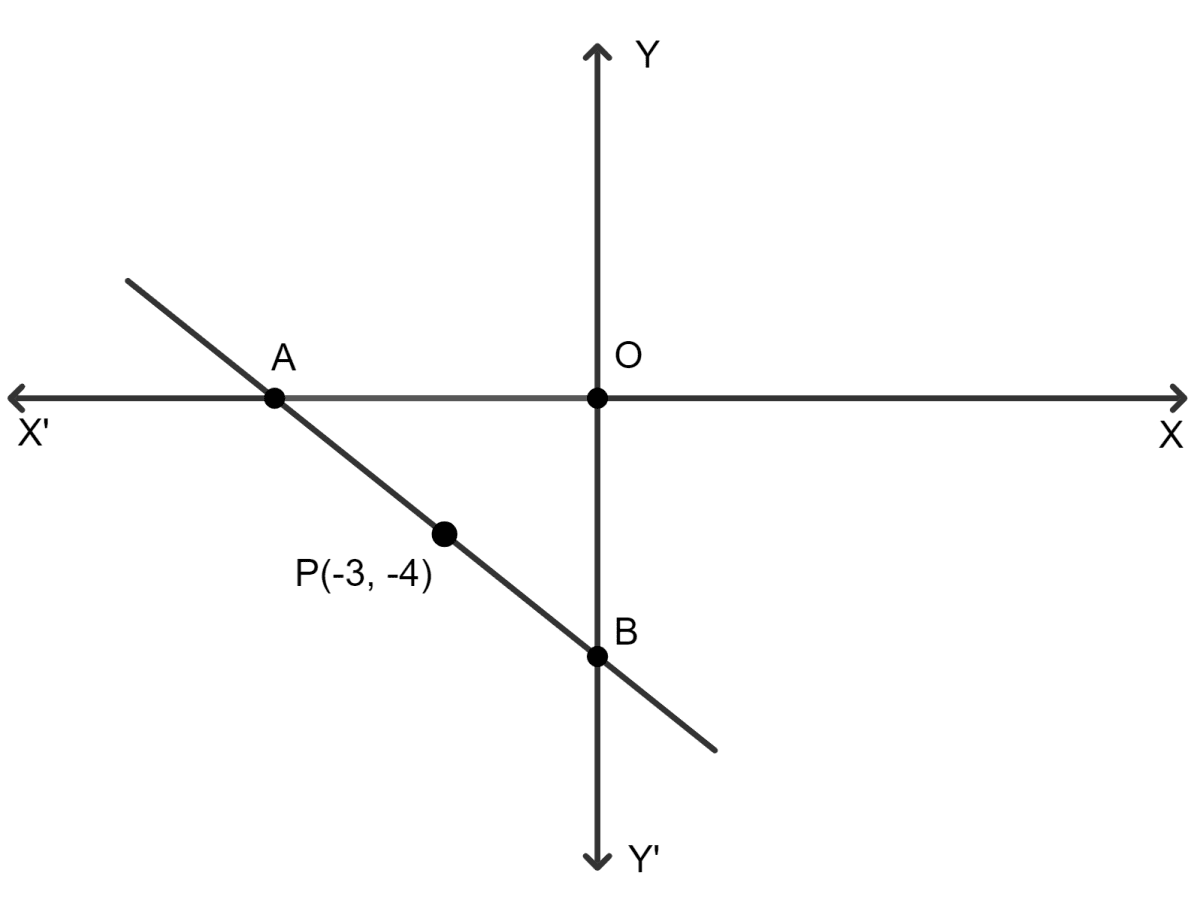
Find the coordinates of points A and B. Also, find the equation of the line passing through the point P and also perpendicular to line-segment AB.
Prove that :
A and B are two events such that P(A) = 0.56 and P(B) = 0.64, find :
(i) P(not A)
(ii) P(not B)
A largest possible sphere is carved out from a solid wooden cube of side 7 cm. Find :
(i) the volume of sphere
(ii) the percentage of wood wasted in the process.
(Take π = )