Mathematics
The quadrilateral formed by angle bisectors of a cyclic quadrilateral is also cyclic. Prove it.
Circles
2 Likes
Answer
Let ABCD be a cyclic quadrilateral and PRQS be the quadrilateral formed by the angle bisectors of angle ∠A, ∠C, ∠B and ∠D.

In ∆APD,
⇒ ∠PAD + ∠ADP + ∠APD = 180° [By angle sum property of a triangle] …..(1)
In ∆BQC,
⇒ ∠QBC + ∠BCQ + ∠BQC = 180° [By angle sum property of a triangle] …..(2)
Adding (1) and (2), we get
⇒ ∠PAD + ∠ADP + ∠APD + ∠QBC + ∠BCQ + ∠BQC = 180° + 180° = 360° …..(3)
From figure,
⇒ ∠PAD + ∠QBC + ∠BCQ + ∠ADP = [∠A + ∠B + ∠C + ∠D]
⇒ ∠PAD + ∠QBC + ∠BCQ + ∠ADP = = 180°
Substituting above value in equation 3 we get :
⇒ ∠APD + ∠BQC + 180° = 360°
⇒ ∠APD + ∠BQC = 360° - 180°
⇒ ∠APD + ∠BQC = 180°
But, these are the sum of opposite angles of quadrilateral PRQS.
∴ PRQS is also a cyclic quadrilateral [As sum of opposite angles in a cyclic quadrilateral = 180°.]
Hence, proved that the quadrilateral formed by angle bisectors of a cyclic quadrilateral is also cyclic.
Answered By
1 Like
Related Questions
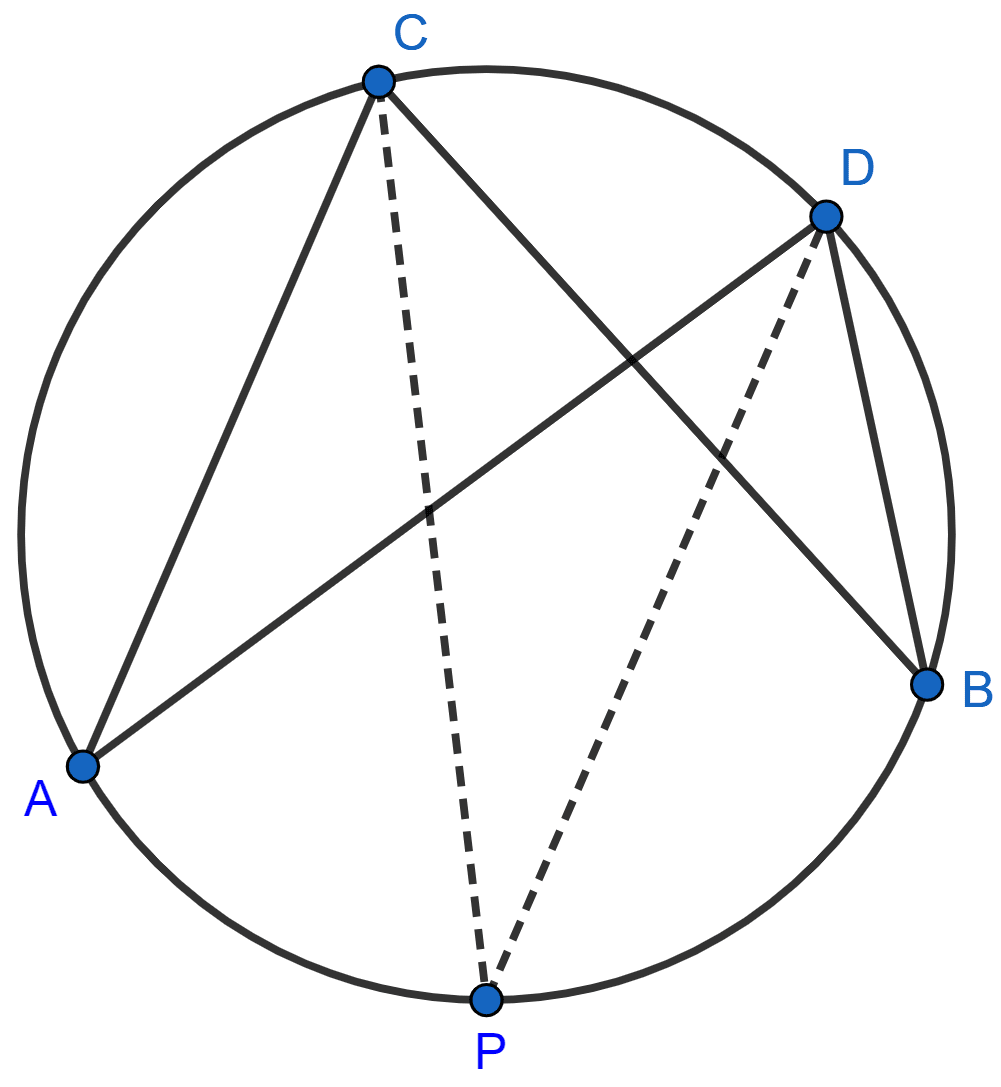
In the figure, given below, CP bisects angle ACB. Show that DP bisects angle ADB.
In the figure, given below, AD = BC, ∠BAC = 30° and ∠CBD = 70°. Find :
(i) ∠BCD
(ii) ∠BCA
(iii) ∠ABC
(iv) ∠ADB

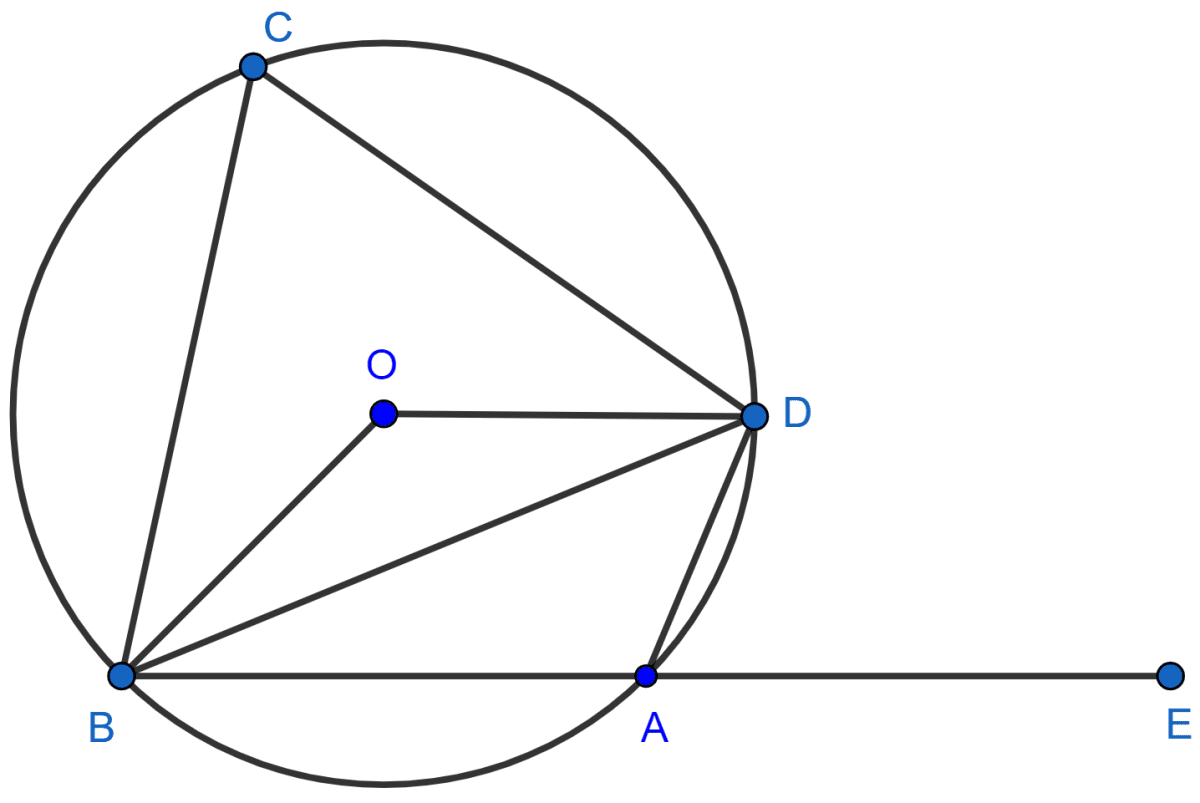
In the given figure, AD is a diameter. O is the centre of the circle. AD is parallel to BC and ∠CBD = 32°. Find :
(i) ∠OBD
(ii) ∠AOB
(iii) ∠BED

In the figure given, O is the centre of the circle. ∠DAE = 70°. Find giving suitable reasons, the measure of
(i) ∠BCD
(ii) ∠BOD
(iii) ∠OBD