The length of the shadow of a tower standing on level plane is found to be 2y meters longer when the sun's altitude is 30° than when it was 45°. Prove that the height of the tower is $y(\sqrt{3} + 1)$ meters.

Let CD be the tower of height h meters and BC be shadow when angle of elevation is 45° and AC be the shadow when angle of elevation is 30°.

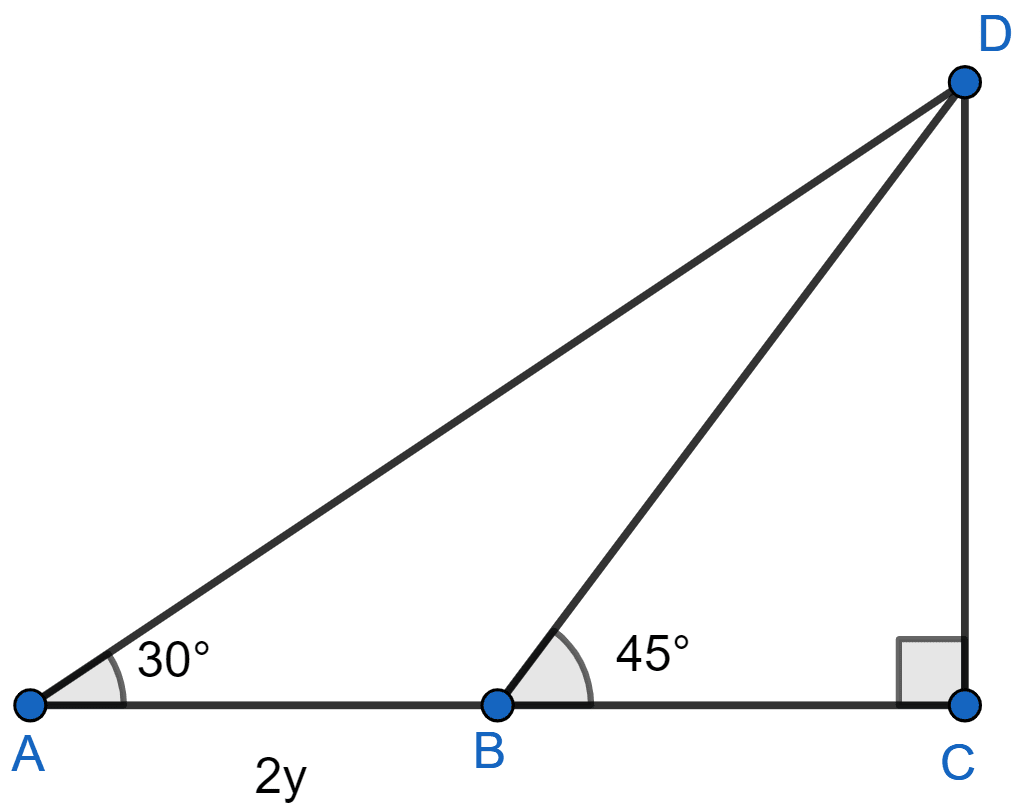
In △ACD,

$\text{tan 30°} = \dfrac{\text{Perpendicular}}{\text{Base}} \\[1em] \Rightarrow \dfrac{1}{\sqrt{3}} = \dfrac{CD}{AC} \\[1em] \Rightarrow \dfrac{1}{\sqrt{3}} = \dfrac{h}{AC} \\[1em] \Rightarrow h = \dfrac{AC}{\sqrt{3}} \text{ m} ………(1)$

In △BCD,

$\text{tan 45°} = \dfrac{\text{Perpendicular}}{\text{Base}} \\[1em] \Rightarrow 1 = \dfrac{CD}{BC} \\[1em] \Rightarrow BC = CD = h$

AC = AB + BC = (2y + h) meters.

Substituting value of AC in equation 1, we get :

$\Rightarrow h = \dfrac{2y + h}{\sqrt{3}} \\[1em] \Rightarrow \sqrt{3}h = 2y + h \\[1em] \Rightarrow \sqrt{3}h - h = 2y \\[1em] \Rightarrow h(\sqrt{3} - 1) = 2y \\[1em] \Rightarrow h = \dfrac{2y}{\sqrt{3} - 1}.$

Multiplying numerator and denominator by $(\sqrt{3} + 1)$.

$\Rightarrow h = \dfrac{2y}{\sqrt{3} - 1} \times \dfrac{\sqrt{3} + 1}{\sqrt{3} + 1} \\[1em] \Rightarrow h = \dfrac{2y(\sqrt{3} + 1)}{(\sqrt{3} - 1)(\sqrt{3} + 1)} \\[1em] \Rightarrow h = \dfrac{2y(\sqrt{3} + 1)}{(\sqrt{3})^2 - 1^2} \\[1em] \Rightarrow h = \dfrac{2y(\sqrt{3} + 1)}{3 - 1} \\[1em] \Rightarrow h = \dfrac{2y(\sqrt{3} + 1)}{2} \\[1em] \Rightarrow h = y(\sqrt{3} + 1).$

Hence, proved that the height of tower = $y(\sqrt{3} + 1)$ meters.