From the top of a hill, the angles of depression of two consecutive kilometer stones, due east are found to be 30° and 45° respectively. Find the distances of the two stones from the foot of hill.

Let C and D be the position of two kilometer stones and AB be the hill.

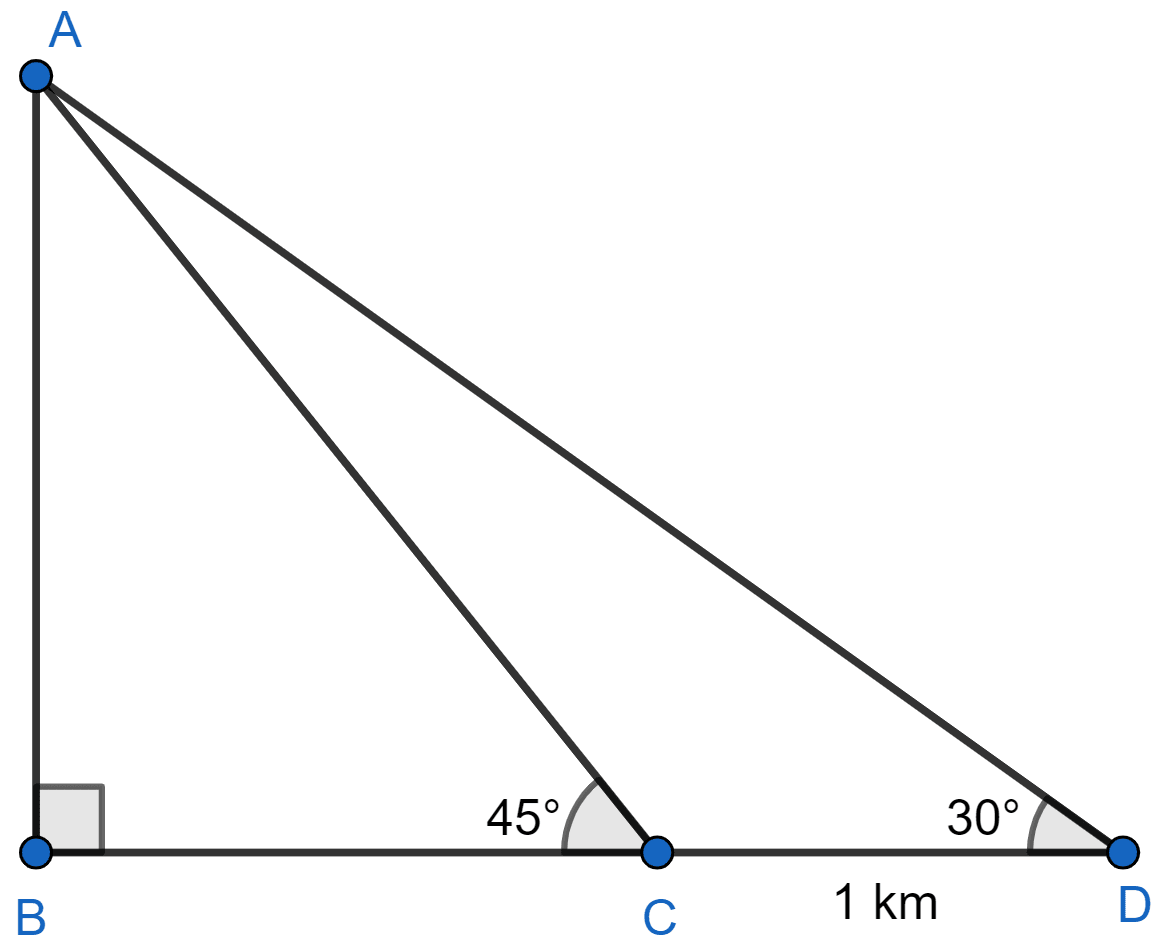
In △ABD,

$\text{tan 30°} = \dfrac{\text{Perpendicular}}{\text{Base}} \\[1em] \Rightarrow \dfrac{1}{\sqrt{3}} = \dfrac{AB}{BD} \\[1em] \Rightarrow BD = \sqrt{3} AB ………(1)$

In △ABC,

$\text{tan 45°} = \dfrac{\text{Perpendicular}}{\text{Base}} \\[1em] \Rightarrow 1 = \dfrac{AB}{BC} \\[1em] \Rightarrow BC = AB …………(2)$

From figure,

⇒ CD = BD - BC

⇒ 1 = $\sqrt{3}AB - AB$

⇒ 1 = $AB(\sqrt{3} - 1)$

⇒ AB = $\dfrac{1}{\sqrt{3} - 1} = \dfrac{1}{0.732}$ = 1.366 km.

From equation (2),

BC = AB = 1.366 km

BD = BC + CD = 1.366 + 1 = 2.366 km.

Hence, kilometer stones are at a distance of 1.366 and 2.366 km.