The height of a cone is 30 cm. A small cone is cut off at the top by a plane parallel to its base. If its volume be $\dfrac{1}{27}$ of the volume of the given cone, at what height above the base is the section cut?

Let OAB be the given cone of height 30 cm and base radius R cm. Let this cone be cut by the plane CND (parallel to the base plane AMB) to obtain cone OCD with height h cm and base radius r cm as shown in the figure below:

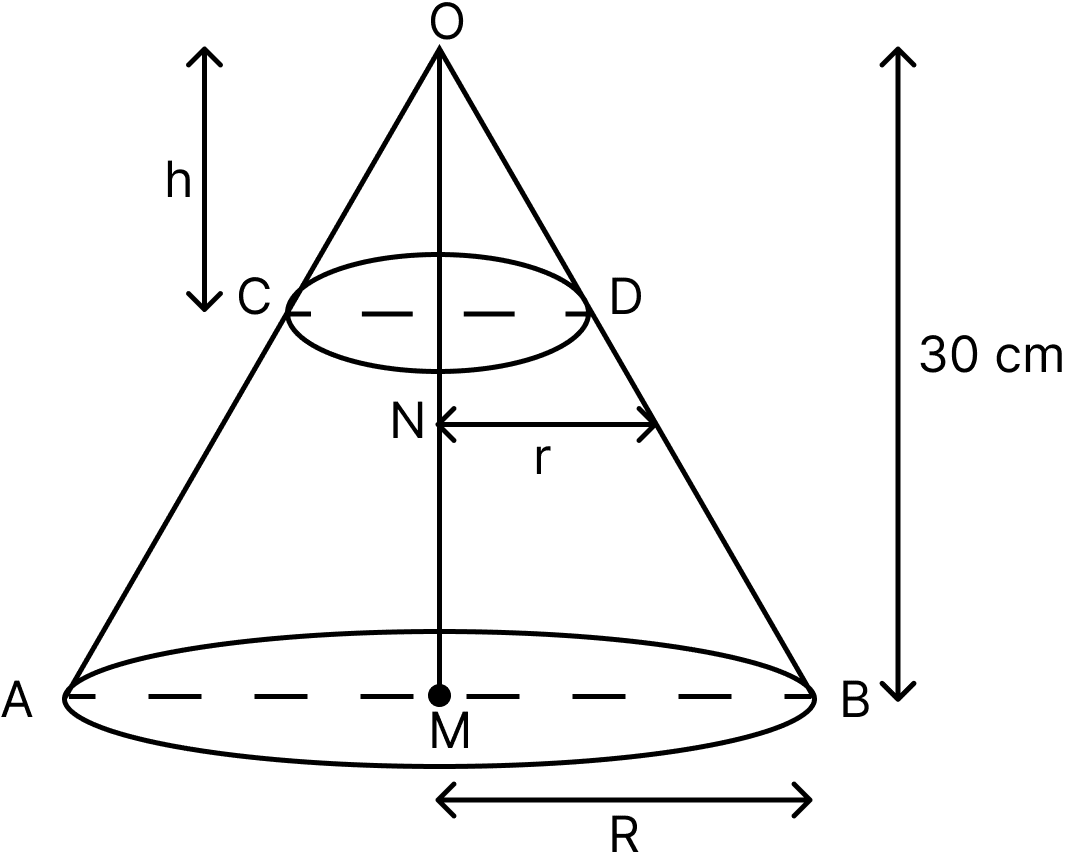
Then △OND ~ △OMB.

∴ $\dfrac{r}{R} = \dfrac{h}{30}$ …..(i)

According to given,

Volume of cone OCD = $\dfrac{1}{27}$ Volume of cone OAB

$\therefore \dfrac{1}{3}πr^2h = \dfrac{1}{27} \times \dfrac{1}{3}πR^2 \times 30$

Dividing both sides by π and multiplying by 3 we get,

$\Rightarrow r^2h = \dfrac{30R^2}{27} \\[1em] \Rightarrow \dfrac{r^2}{R^2} = \dfrac{30}{27h} \\[1em] \Rightarrow \Big(\dfrac{r}{R}\Big)^2 = \dfrac{10}{9h}.$

Using (i)

$\Rightarrow \Big(\dfrac{h}{30}\Big)^2 = \dfrac{10}{9h} \\[1em] \Rightarrow \dfrac{h^2}{900} = \dfrac{10}{9h} \\[1em] \Rightarrow h^3 = \dfrac{10 \times 900}{9} \\[1em] \Rightarrow h^3 = 10 \times 100 \\[1em] \Rightarrow h^3 = 1000 \\[1em] \Rightarrow h^3 = 10^3 \\[1em] \Rightarrow h = 10 \text{ cm}.$

The height of the cone OCD = 10 cm.

∴ The section is cut at the height of (30 - 10) cm = 20 cm.

Hence, the section cut is above 20 cm from the base.