Mathematics
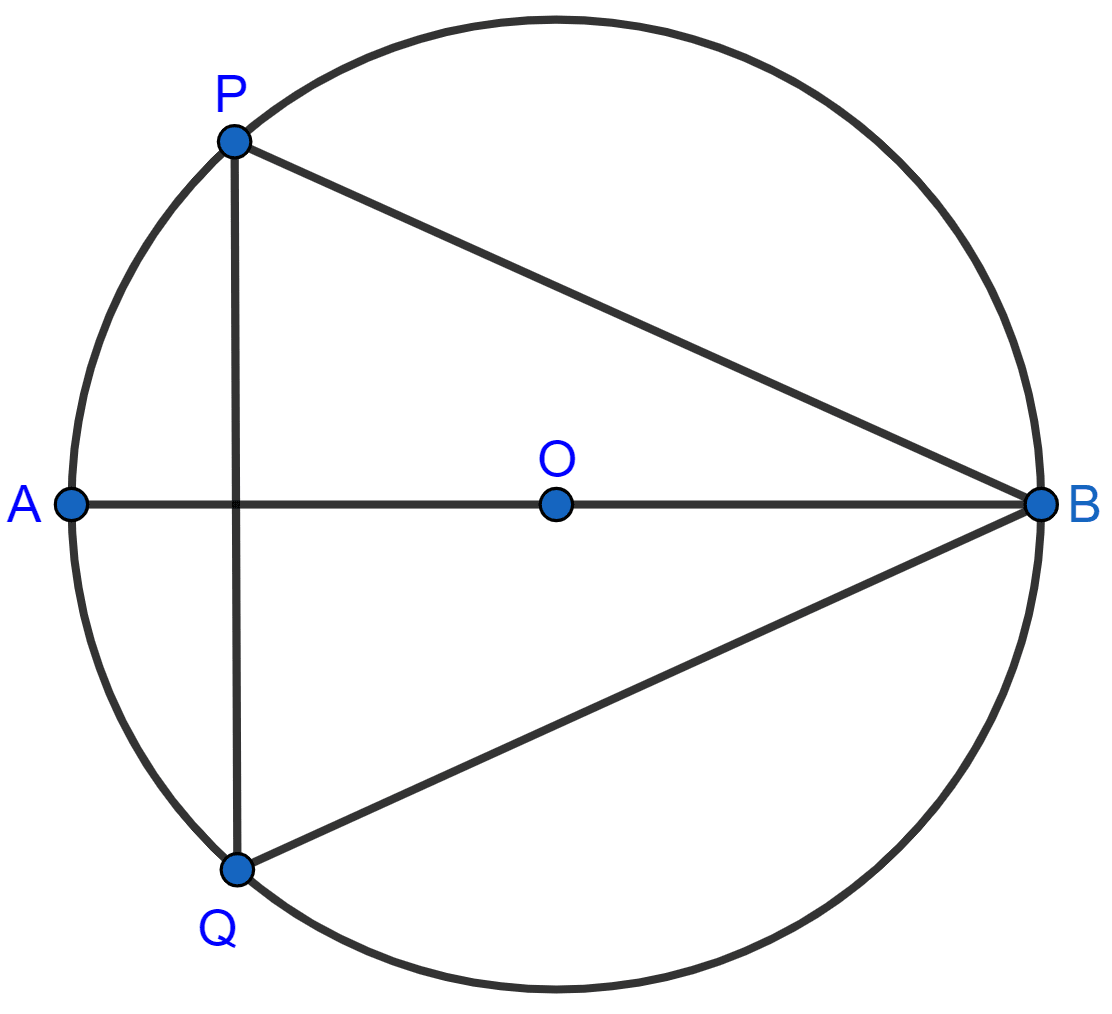
The given figure shows a circle with center O and ∠ABP = 42°. Calculate the measure of :
(i) ∠PQB
(ii) ∠QPB + ∠PBQ
Circles
30 Likes
Answer
Join AP.
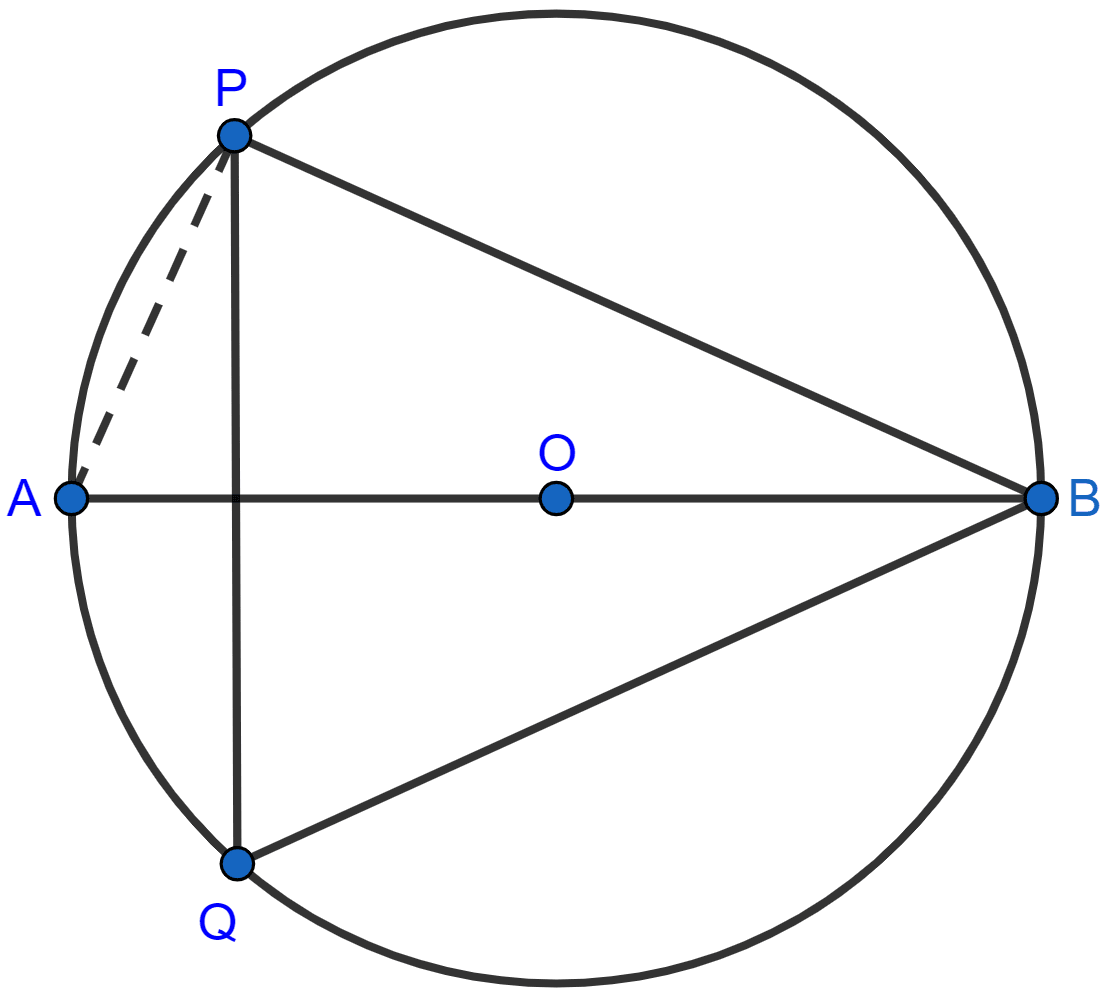
(i) We know that,
Angle in a semi-circle is a right angle.
∠APB = 90°.
In △APB,
⇒ ∠APB + ∠ABP + ∠BAP = 180° [Angle sum property of triangle]
⇒ 90° + 42° + ∠BAP = 180°
⇒ ∠BAP + 132° = 180°
⇒ ∠BAP = 180° - 132° = 48°.
From figure,
∠PQB = ∠BAP = 48° [Angles in same segment are equal]
Hence, ∠PQB = 48°.
(ii) In △BQP,
⇒ ∠QPB + ∠PBQ + ∠PQB = 180° [Angle sum property of triangle]
⇒ ∠QPB + ∠PBQ + 48° = 180°
⇒ ∠QPB + ∠PBQ = 180° - 48°
⇒ ∠QPB + ∠PBQ = 132°.
Hence, ∠QPB + ∠PBQ = 132°.
Answered By
20 Likes
Related Questions
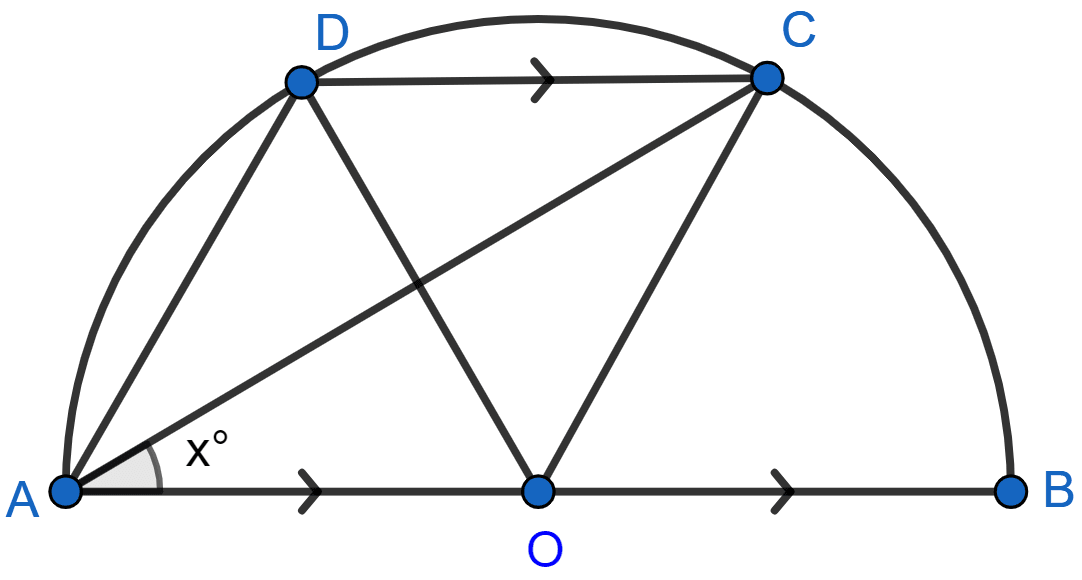
In the given figure, AOB is a diameter and DC is parallel to AB. If ∠CAB = x°; find (in terms of x) the values of :
(i) ∠COB,
(ii) ∠DOC,
(iii) ∠DAC,
(iv) ∠ADC.
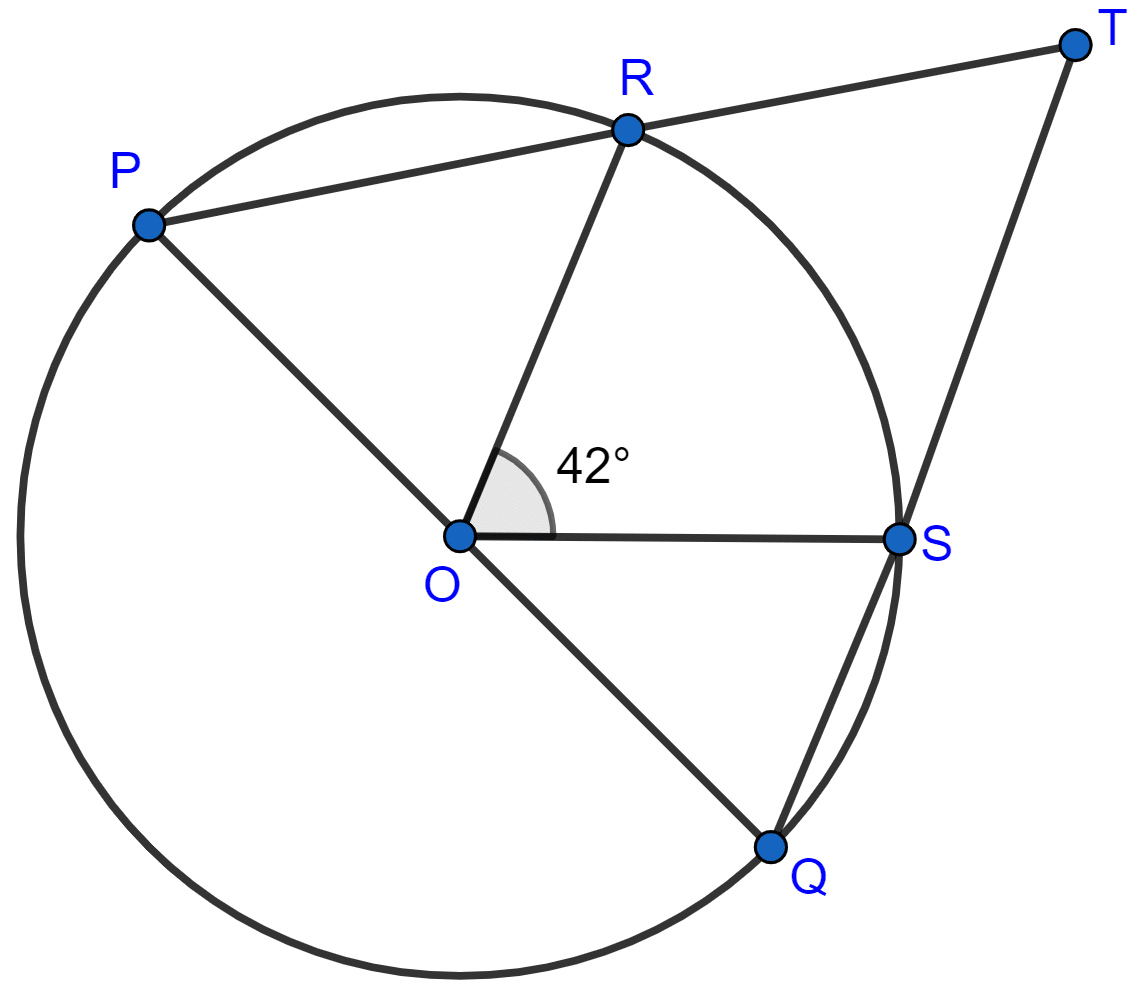
In the given figure, PQ is the diameter of the circle whose center is O. Given, ∠ROS = 42°, calculate ∠RTS.
In the given figure, M is the centre of the circle. Chords AB and CD are perpendicular to each other. If ∠MAD = x and ∠BAC = y :
(i) express ∠AMD in terms of x.
(ii) express ∠ABD in terms of y.
(iii) prove that : x = y.

ABCD is a trapezium with AD parallel to BC. Side BC is produced to point E and angle DCE = 95°. Angle B is equal to :
85°
105°
95°
175°
