Mathematics
The following figure shows a parallelogram ABCD whose side AB is parallel to the x-axis, ∠A = 60° and vertex C = (7, 5). Find the equations of BC and CD.

Straight Line Eq
22 Likes
Answer
Given, ∠A = 60° and vertex C = (7, 5)

As, ABCD is a parallelogram, we have
∠A + ∠B = 180° [Sum of adjacent angles in a || gm = 180°]
∠B = 180° – 60° = 120°
So, the anticlockwise angle of BC from x-axis is (180° - 120°) = 60°.
Slope of BC = tan 60° =
By point-slope form,
Equation of line BC is :
⇒ y – y1 = m(x – x1)
⇒ y – 5 = (x – 7)
⇒ y – 5 =
⇒ y =
As, CD || AB and AB || x-axis
Slope of CD = Slope of AB = 0 [As slope of x-axis is zero]
By point-slope form,
Equation of line CD is :
⇒ y – y1 = m(x – x1)
⇒ y – 5 = 0(x – 7)
⇒ y = 5.
Hence, equation of BC is y = and CD is y = 5.
Answered By
17 Likes
Related Questions
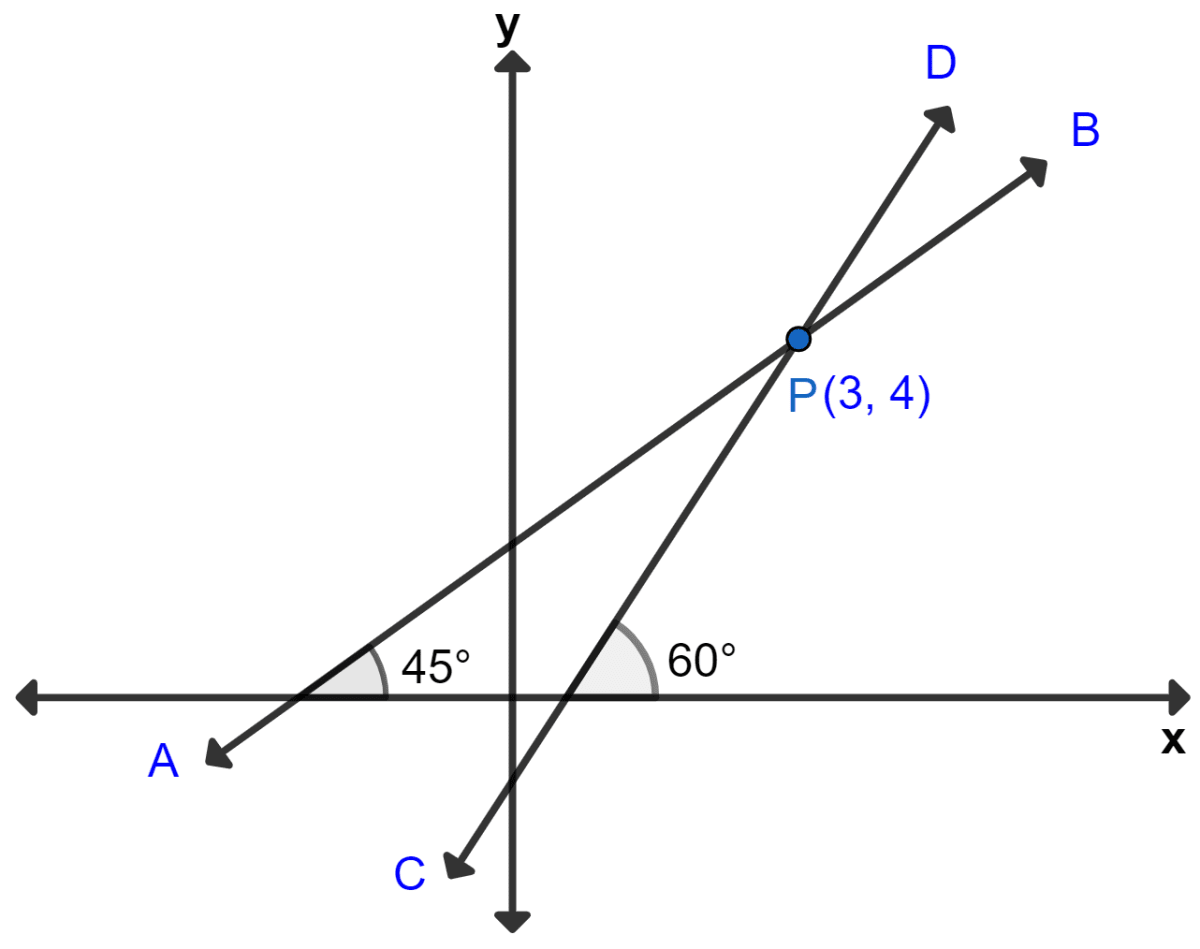
The figure given alongside shows two straight lines AB and CD intersecting each other at point P (3, 4). Find the equations of AB and CD.
In △ABC, A (3, 5), B (7, 8) and C (1, -10). Find the equation of the median through A.
Find the equation of the straight line passing through origin and the point of intersection of the lines x + 2y = 7 and x - y = 4.
In triangle ABC, the co-ordinates of vertices A, B and C are (4, 7), (-2, 3) and (0, 1) respectively. Find the equation of median through vertex A.
Also, find the equation of the line through vertex B and parallel to AC.