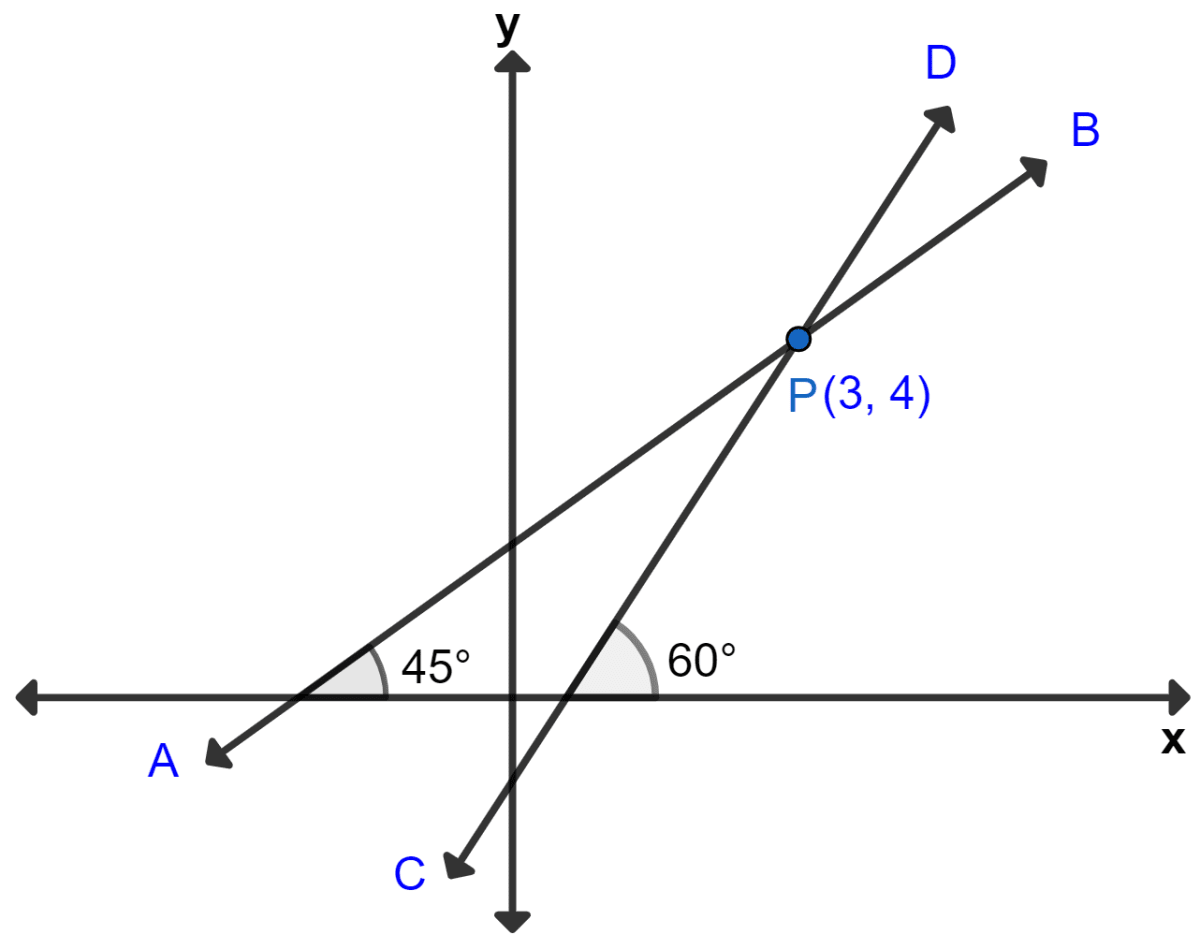
The figure given alongside shows two straight lines AB and CD intersecting each other at point P (3, 4). Find the equations of AB and CD.

From figure,

Slope of AB = tan 45° = 1.

Slope of CD = tan 60° = $\sqrt{3}$.

By point-slope form,

$y - y$1 = m(x - x1)

Since, line AB passes through point P(3, 4) and slope = 1. Substituting values in point-slope form,

⇒ y - 4 = 1(x - 3)

⇒ y - 4 = x - 3

⇒ y - x = -3 + 4

⇒ y - x = 1

⇒ y = x + 1.

Since, line CD passes through point P(3, 4) and slope = $\sqrt{3}$. Substituting values in point-slope form,

⇒ y - 4 = $\sqrt{3}$(x - 3)

⇒ y - 4 = $\sqrt{3}x - 3\sqrt{3}$

⇒ y = $\sqrt{3}x - 3\sqrt{3} + 4$.

Hence, equation of AB is y = x + 1 and equation of CD is y = $\sqrt{3}x - 3\sqrt{3} + 4$.