Mathematics
The co-ordinates of two points P and Q are (2, 6) and (-3, 5) respectively. Find :
(i) the gradient of PQ;
(ii) the equation of PQ;
(iii) the co-ordinates of the point where PQ intersects the x-axis.
Straight Line Eq
16 Likes
Answer
(i) By formula,
Slope =
Substituting values we get,
Hence, gradient of slope PQ = .
(ii) By point slope form,
Equation : y - y1 = m(x - x1)
⇒ y - 6 = (x - 2)
⇒ 5(y - 6) = x - 2
⇒ 5y - 30 = x - 2
⇒ 5y = x - 2 + 30
⇒ 5y = x + 28
Hence, equation of PQ is 5y = x + 28.
(iii) The point where PQ intersects x-axis, there y co-ordinate = 0.
Substituting y = 0 in equation of PQ we get,
⇒ 5 × 0 = x + 28
⇒ 0 = x + 28
⇒ x = -28.
Point = (x, y) = (-28, 0).
Hence, co-ordinates of the point where PQ intersects the x-axis = (-28, 0).
Answered By
11 Likes
Related Questions
Find the equation of a line which passes through (5, 4) and makes an angle of 60° with the positive direction of the x-axis.
Find the equation of a line passing through :
(i) (0, 1) and (1, 2)
(ii) (-1, -4) and (3, 0)
The co-ordinates of two points A and B are (-3, 4) and (2, -1). Find :
(i) the equation of AB;
(ii) the co-ordinates of the point where the line AB intersects the y-axis.
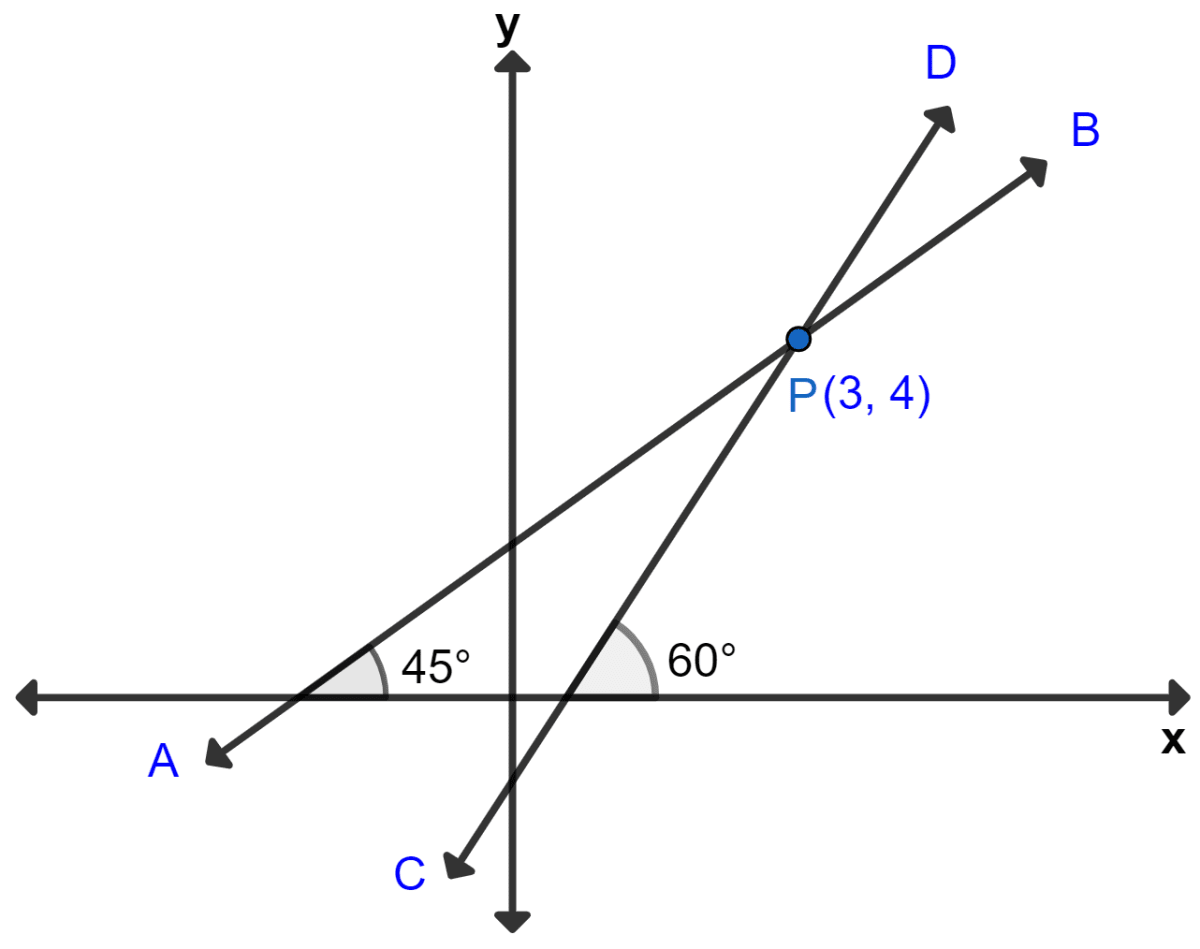
The figure given alongside shows two straight lines AB and CD intersecting each other at point P (3, 4). Find the equations of AB and CD.