Mathematics
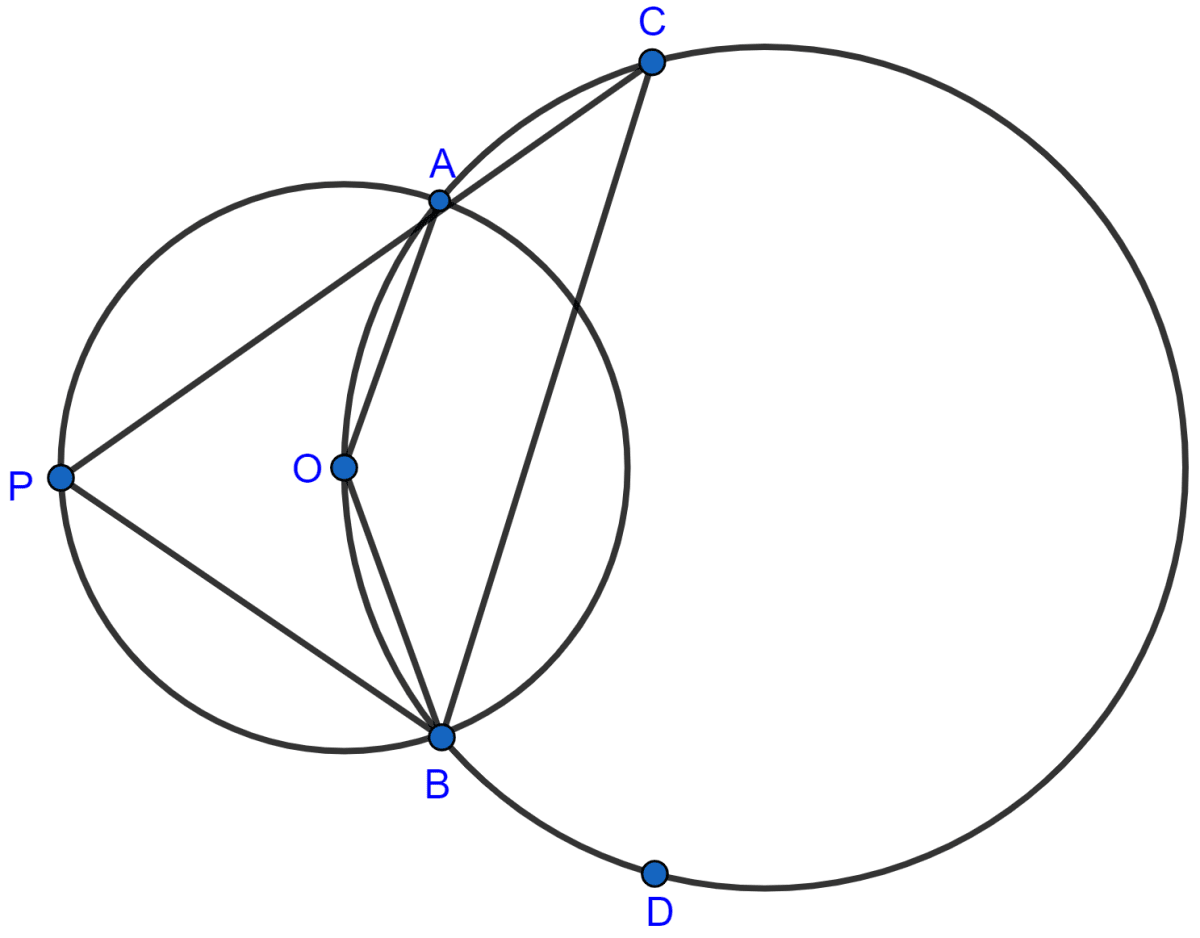
The figure shows two circles which intersect at A and B. The center of the smaller circle is O and lies on the circumference of the larger circle. Given ∠APB = a°.
Calculate, in terms of a°, the value of :
(i) obtuse ∠AOB,
(ii) ∠ACB,
(iii) ∠ADB.
Give reasons for your answers clearly.
Answer
(i) We know that,
Angle at the center is double the angle at the circumference subtended by the same chord.
obtuse ∠AOB = 2∠APB = 2a°.
Hence, obtuse ∠AOB = 2a°.
(ii) OACB is a cyclic quadrilateral.
⇒ ∠AOB + ∠ACB = 180° [Sum of opposite angles in a cyclic quadrilateral = 180°.]
⇒ ∠ACB + 2a° = 180°
⇒ ∠ACB = 180° - 2a°.
Hence, ∠ACB = 180° - 2a°.
(iii) Join AD and BD.
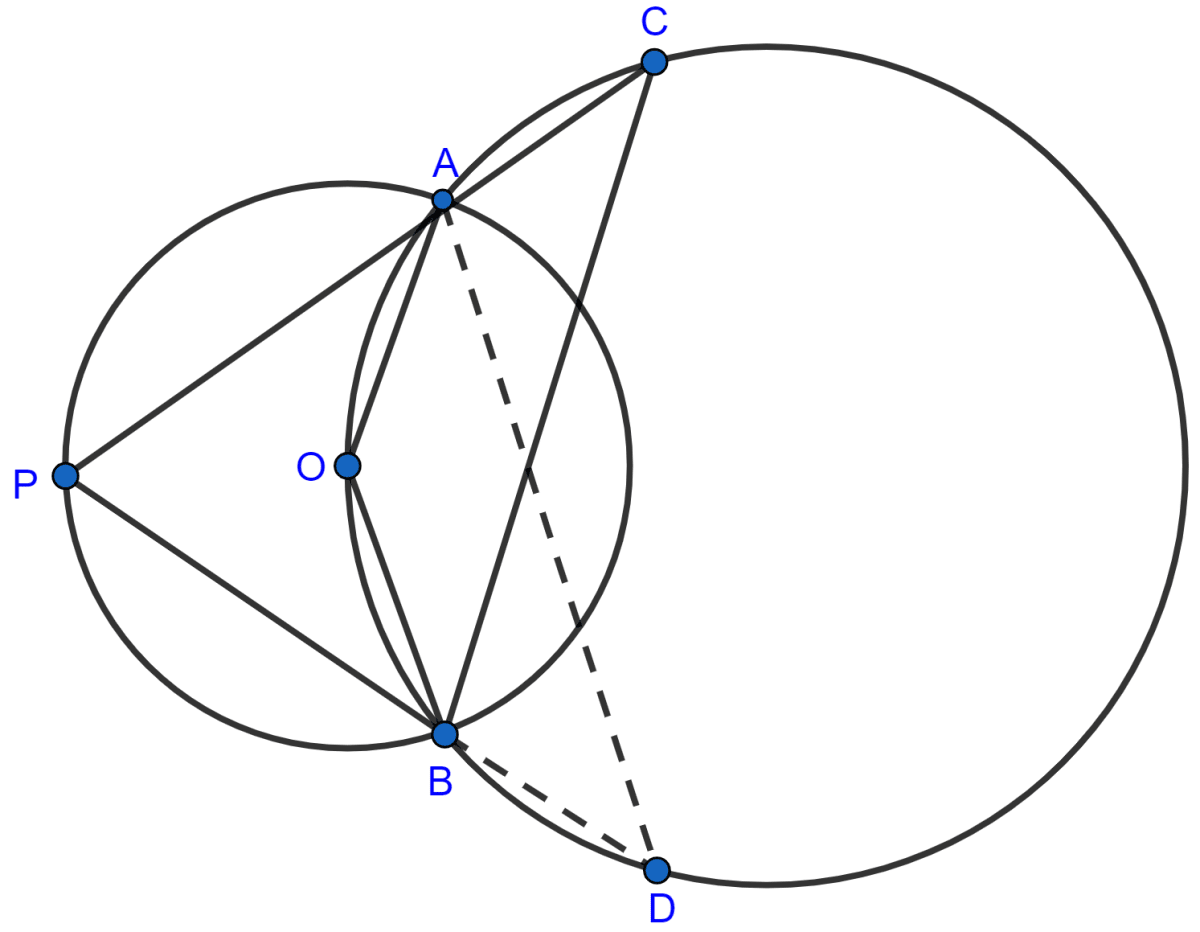
As, angles in same segment are equal.
∴ ∠ADB = ∠ACB = 180° - 2a°.
Hence, ∠ADB = 180° - 2a°.
Related Questions
ABCD is a cyclic quadrilateral in which AB is parallel to DC and AB is a diameter of the circle. Given ∠BED = 65°; calculate :
(i) ∠DAB,
(ii) ∠BDC.

In the given figure, O is the centre of the circle and ∠ABC = 55°. Calculate the values of x and y.

In the figure, O is the center of the circle, ∠AOE = 150°, ∠DAO = 51°. Calculate the sizes of the angles CEB and OCE.
In the figure, given below, P and Q are the centers of two circles intersecting at B and C. ACD is a straight line. Calculate the numerical value of x.
