The diagram given below shows a ski jump. A skier weighing 60kgf stands at A at the top of ski jump. He moves from A and takes off for his jump at B.

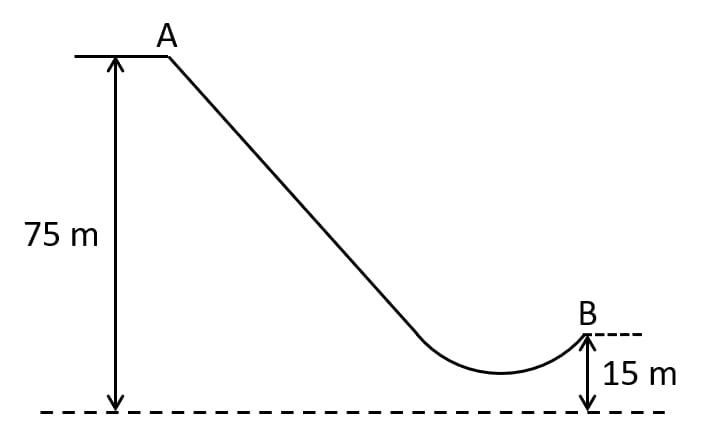
(a) Calculate the change in the gravitational potential energy of the skier between A and B.

(b) If 75% of the energy in part (a) becomes the kinetic energy at B, calculate the speed at which the skier arrives at B.

(Take g = 10 ms^-2).

(c) Does total mechanical energy change during the ski jump?

Given,

Mass = 60 kg

(a)

$\text {Loss in potential energy} = \text{mg (h1 – h2)} \\[0.5em] = 60 \times 10\times (75-15) \\[0.5em] = 60 \times10 \times 60 \\[0.5em] = 3.6 \times 10^4 J \\[0.5em]$

(b) When kinetic energy at B is 75% of (3.6 × 10⁴)

$\text{Kinetic energy at B} = \dfrac{75}{100} \times 3.6 \times 10^4 \\[0.5em] = 27000J \\[0.5em] = 2.7 \times 10^4 J \\[0.5em]$

Since,

Kinetic energy = $\dfrac{1}{2}$ mv²

Substituting the values in equation we get,

$27000 = \dfrac{1}{2} \times 60 \times v^2 \\[0.5em] \Rightarrow 27000 = 1 \times 30 \times v^2 \\[0.5em] \Rightarrow v^2 = \dfrac{27000}{30} \\[0.5em] \Rightarrow v^2 = 900 \\[0.5em] \Rightarrow v = \sqrt{900} \\[0.5em] \Rightarrow v = 30 \\[0.5em]$

∴ The speed at which the skier arrives at B = 30ms^-1

(c) As there is an interchange between potential energy and kinetic energy and all kinds of frictional forces are absent so the total mechanical energy remains constant, hence no change in mechanical energy occurs.