The angle of elevation of the top of a tower is observed to be 60°. At a point, 30 m vertically above the first point of observation, the elevation is found to be 45°. Find:

(i) the height of the tower,

(ii) its horizontal distance from the points of observation.

(i) Let AB be the the tower, C be the first point of observation and D be the second point.

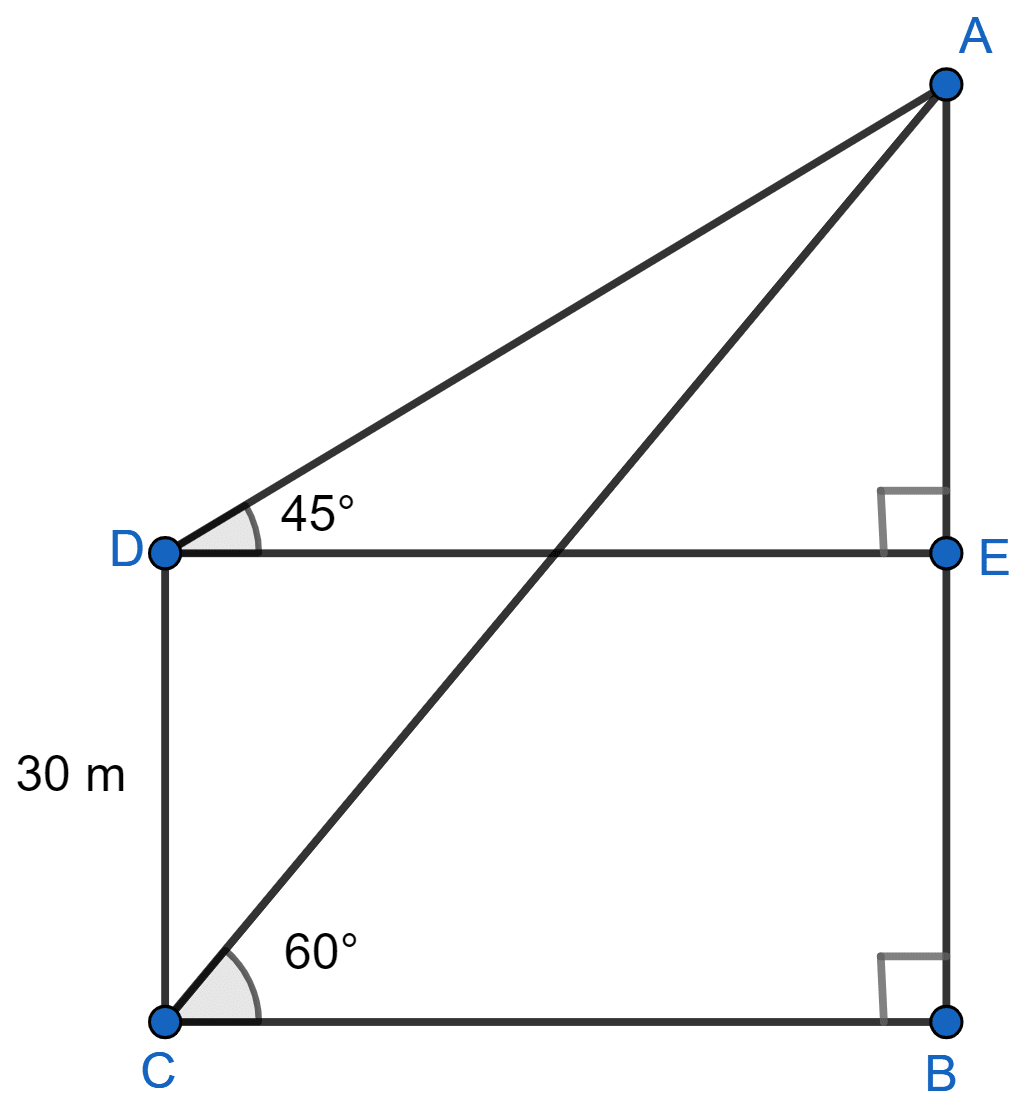
From figure,

BC = ED = a (let) and BE = CD = 30 m.

In △ABC,

$\text{tan 60°} = \dfrac{\text{Perpendicular}}{\text{Base}} \\[1em] \Rightarrow \sqrt{3} = \dfrac{AB}{BC}\\[1em] \Rightarrow AB = \sqrt{3}BC \\[1em] \Rightarrow AB = \sqrt{3}a ……….(1)$

In △AED,

$\text{tan 45°} = \dfrac{\text{Perpendicular}}{\text{Base}} \\[1em] \Rightarrow 1 = \dfrac{AE}{ED}\\[1em] \Rightarrow AE = ED \\[1em] \Rightarrow AE = a ……….(2)$

We know that,

⇒ CD = AB - AE

⇒ 30 = $\sqrt{3}a - a$

⇒ 30 = $a(\sqrt{3} - 1)$

⇒ a = $\dfrac{30}{\sqrt{3} - 1} = \dfrac{30}{1.732 - 1} = \dfrac{30}{0.732}$ = 40.98 metres.

From equation (1),

AB = $\sqrt{3}a = 1.732 \times$ 40.98 = 70.98 meters.

Hence, height of tower = 70.98 meters.

(ii) From part (i),

ED = a = 40.98 meters.

Hence, horizontal distance from the points of observation is 40.98 meters.