Two pillars of equal heights stand on either side of a roadway, which is 150 m wide. At a point in the roadway between the pillars the elevations of the tops of the pillars are 60° and 30°; find the height of the pillars and the position of the point.

Let AB and CD be the two towers of height h meters. Let P be a point in the roadway BD such that BD = 150 m, ∠APB = 60° and ∠CPD = 30°.

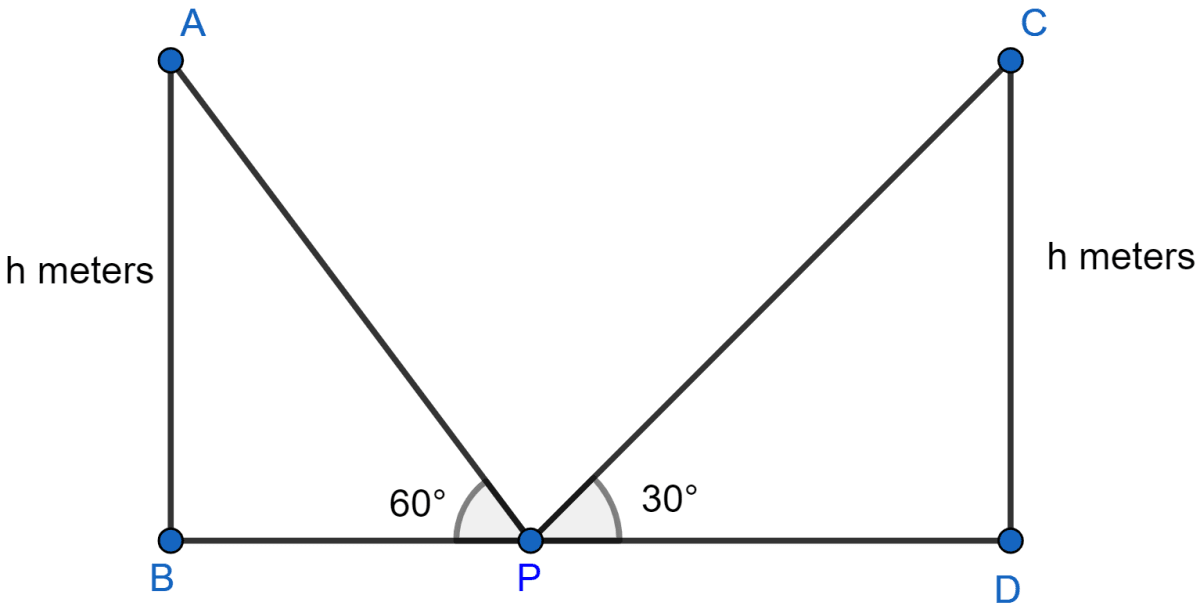
In ∆ABP,

$\text{tan 60°} = \dfrac{\text{Perpendicular}}{\text{Base}} \\[1em] \Rightarrow \sqrt{3} = \dfrac{AB}{BP} \\[1em] \Rightarrow BP = \dfrac{AB}{\sqrt{3}} \\[1em] \Rightarrow BP = \dfrac{h}{\sqrt{3}}\space …………(1)$

In ∆CDP,

$\text{tan 30°} = \dfrac{\text{Perpendicular}}{\text{Base}} \\[1em] \Rightarrow \dfrac{1}{\sqrt{3}} = \dfrac{CD}{PD} \\[1em] \Rightarrow PD = \sqrt{3}CD \\[1em] \Rightarrow PD = \sqrt{3}h\space …………(2)$

We know that,

⇒ BD = 150 m

⇒ BP + PD = 150 m

From (1) and (2), we get :

$\Rightarrow \dfrac{h}{\sqrt{3}} + \sqrt{3}h = 150 \\[1em] \Rightarrow \dfrac{h + 3h}{\sqrt{3}} = 150 \\[1em] \Rightarrow \dfrac{4h}{\sqrt{3}} = 150 \\[1em] \Rightarrow 4h = 150 \times \sqrt{3} \\[1em] \Rightarrow h = \dfrac{150 \times 1.732}{4} \\[1em] \Rightarrow h = 37.5 \times 1.732 \\[1em] \Rightarrow h = 64.95 \text{ meters}.$

From equation (1),

BP = $\dfrac{h}{\sqrt{3}} = \dfrac{64.95}{1.732}$ = 37.5 meters.

Hence, height of each pillar is 64.95 m and the point P is 37.5 m from the pillar AB.