A man on a cliff observes a boat, at an angle of depression 30°, which is sailing towards the shore to the point immediately beneath him. Three minutes later, the angle of depression of the boat is found to be 60°. Assuming that the boat sails at a uniform speed, determine :

(i) how much more time it will take to reach the shore ?

(ii) the speed of the boat in metre per second, if the height of the cliff is 500 m.

Let CD be the cliff and A be the position of the ship when angle of elevation is 30° and B be the position when angle of elevation is 60°.

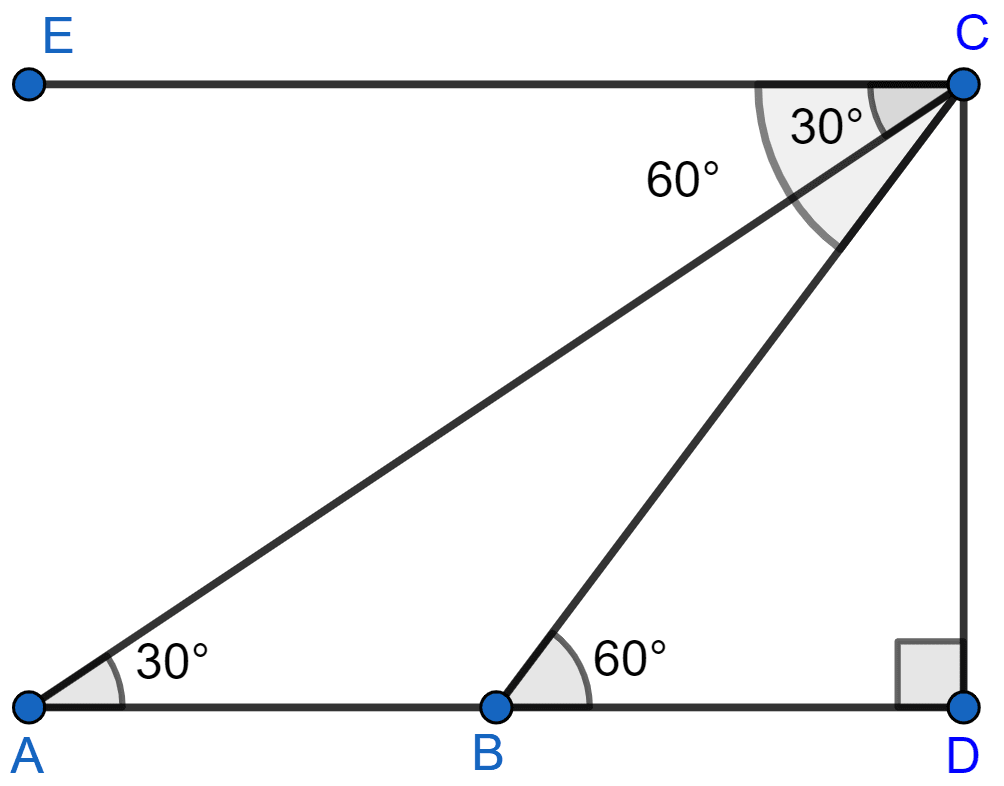
(i) From figure,

$\text{tan 60°} = \dfrac{\text{Perpendicular}}{\text{Base}} \\[1em] \Rightarrow \sqrt{3} = \dfrac{CD}{BD} \space ………….(1) \\[1em] \text{tan 30°} = \dfrac{\text{Perpendicular}}{\text{Base}} \\[1em] \Rightarrow \dfrac{1}{\sqrt{3}} = \dfrac{CD}{AD} \space ………….(2)$

Dividing equation (1) by (2), we get :

$\Rightarrow \dfrac{\sqrt{3}}{\dfrac{1}{\sqrt{3}}} = \dfrac{\dfrac{CD}{BD}}{\dfrac{CD}{AD}} \\[1em] \Rightarrow \sqrt{3} \times \sqrt{3} = \dfrac{AD}{BD} \\[1em] \Rightarrow \dfrac{AD}{BD} = 3 \\[1em] \Rightarrow AD = 3BD \\[1em] \Rightarrow AB + BD = 3BD \\[1em] \Rightarrow AB = 2BD.$

Boat reaches from point A to B in 3 minutes.

Thus, boat covers distance AB in 3 minutes or it covers distance

⇒ 2 BD in 3 minutes

⇒ BD in $\dfrac{3}{2}$ = 1.5 minutes.

Hence, it will takes 1.5 minutes more to reach the shore.

(ii) In △ADC,

$\text{tan 30°} = \dfrac{\text{Perpendicular}}{\text{Base}} \\[1em] \Rightarrow \dfrac{1}{\sqrt{3}} = \dfrac{CD}{AD} \\[1em] \Rightarrow AD = \sqrt{3}CD$

In △BDC,

$\text{tan 60°} = \dfrac{\text{Perpendicular}}{\text{Base}} \\[1em] \Rightarrow \sqrt{3} = \dfrac{CD}{BD} \\[1em] \Rightarrow BD = \dfrac{CD}{\sqrt{3}}$

From figure,

$\Rightarrow AB = AD - BD \\[1em] \Rightarrow AB = \sqrt{3}CD - \dfrac{CD}{\sqrt{3}} \\[1em] \Rightarrow AB = \dfrac{3CD - CD}{\sqrt{3}} \\[1em] \Rightarrow AB = \dfrac{2CD}{\sqrt{3}} ………(1)$

Let speed of boat be a meter/second so in 3 minutes boat will travel :

Distance (AB) = Speed × Time

AB = a × 3 × 60

AB = 180a meters ………(2)

From (1) and (2) we get,

$\Rightarrow \dfrac{2CD}{\sqrt{3}} = 180a \\[1em] \Rightarrow \dfrac{2 \times 500}{\sqrt{3}} = 180a \\[1em] \Rightarrow \dfrac{1000}{1.732} = 180a \\[1em] \Rightarrow a = \dfrac{1000}{180 \times 1.732} \\[1em] \Rightarrow a = \dfrac{1000}{311.76} = 3.21 \text{ m/s}.$

Hence, speed of boat = 3.21 m/s.