The angle of elevation of a cloud from a point h metres above the surface of a lake is θ and the angle of depression of its reflection in the lake is Φ. Prove that the height of the cloud above the lake surface is : $h\Big(\dfrac{\text{tan Φ + tan θ}}{\text{tan Φ - tan θ}}\Big)$.

In the figure shown below:

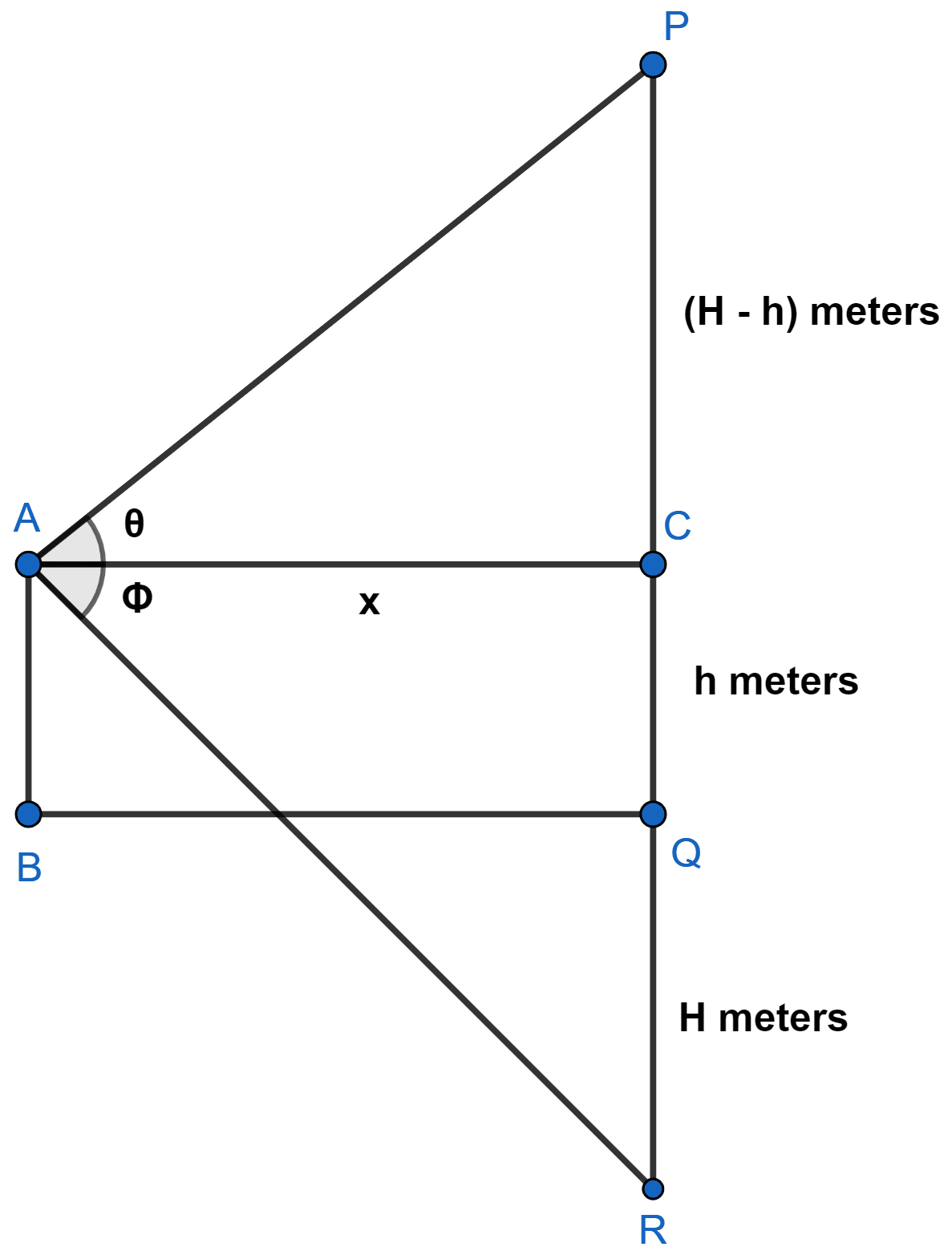
Let BQ be the surface of lake, P be the cloud and R be its reflection in lake.

Let H metres be the height of the cloud above water level. The distance of the reflection is same as that of the cloud from the lake surface.

PQ = QR = H meters

Let A be the point h meters above the surface of the lake from where angle of elevation is θ.

Let AB = h metres, AC = BQ = x

In △ACP,

tan θ = $\dfrac{PC}{AC}$

Substituting values we get :

$\Rightarrow \text{tan θ} = \dfrac{H- h}{x} \\[1em] \Rightarrow x = \dfrac{H - h}{\text{tan θ}} \text{ …….. (1)}$

tan Φ = $\dfrac{RC}{AC}$

Substituting values we get :

$\Rightarrow \text{tan Φ} = \dfrac{H + h}{x} \\[1em] \Rightarrow x = \dfrac{H + h}{\text{tan Φ}} \text{ …….. (2)}$

From (1) and (2), we have :

$\Rightarrow \dfrac{H - h}{\text{tan θ}} = \dfrac{H + h}{\text{tan Φ}} \\[1em] \Rightarrow (H - h)\text{ tan Φ} = (H + h)\text{ tan θ} \\[1em] \Rightarrow \text{H tan Φ - h tan Φ} = \text{H tan θ + h tan θ} \\[1em] \Rightarrow \text{H tan Φ - H tan θ} = \text{h tan θ + h tan Φ} \\[1em] \Rightarrow H\text{(tan Φ - tan θ)} = h\text{(tan θ + tan Φ)} \\[1em] \Rightarrow H = \text{h}\dfrac{\text{(tan θ + tan Φ)}}{\text{(tan Φ - tan θ)}}.$

Hence, proved that the height of the cloud above the lake surface is $h\Big(\dfrac{\text{tan Φ + tan θ}}{\text{tan Φ - tan θ}}\Big)$.